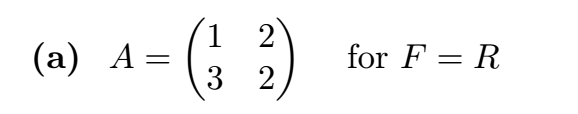
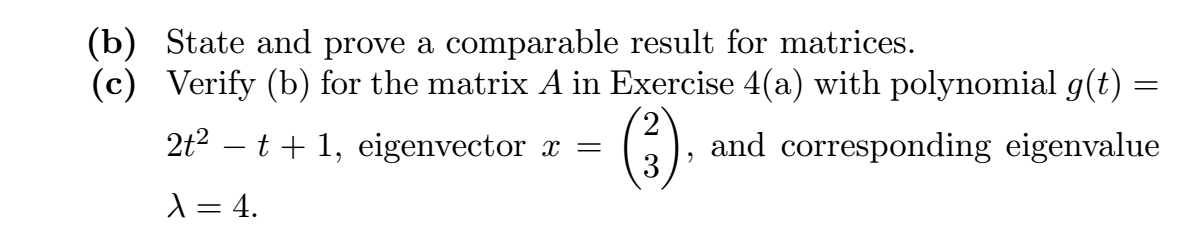
\f22. (a) Let T be a linear operator on a vector space V over the field F, and let g(t) be a polynomial with coefficients from F. Prove that if x is an eigenvector of T with corresponding eigenvalue 1, then g(T)(x) = g(X)x. That is, x is an eigenvector of g(T) with corre- sponding eigenvalue g(1).(b) State and prove a comparable result for matrices. (c) Verify (b) for the matrix A in Exercise 4(a) with polynomial g(t) = 2 2t2 t + 1, eigenvector at = (3 A24. ), and corresponding eigenvalue