Question: f(3) (5 marks) Let fn(x) = n By appealing to Corollary 4.26, Theorem 4.24, and the Archimedean Principle, prove (fn(x)) converges pointwise to f(x) =
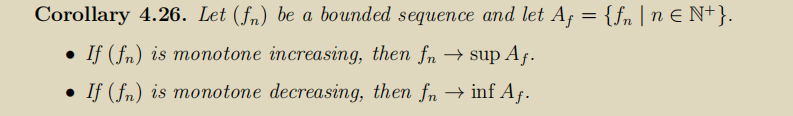
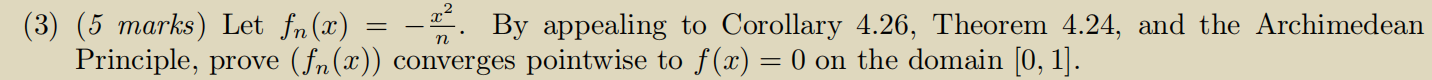
![f(x) = 0 on the domain [0, 1].Theorem 4.24. Let A C](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667cb77b79183_467667cb77b66f37.jpg)
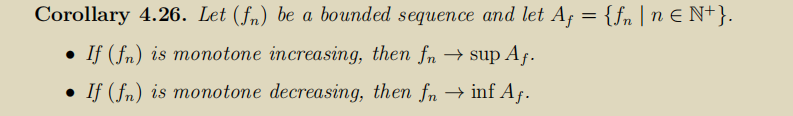
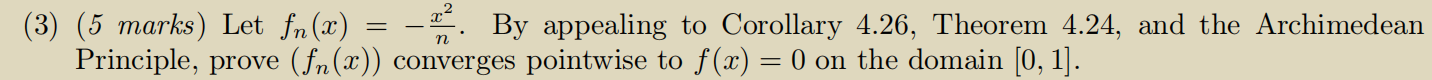
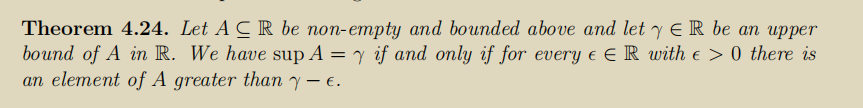
\f(3) (5 marks) Let fn(x) = n By appealing to Corollary 4.26, Theorem 4.24, and the Archimedean Principle, prove (fn(x)) converges pointwise to f(x) = 0 on the domain [0, 1].Theorem 4.24. Let A C R be non-empty and bounded above and let y E R be an upper bound of A in R. We have sup A = y if and only if for every c E R with e > 0 there is an element of A greater than y - E
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


