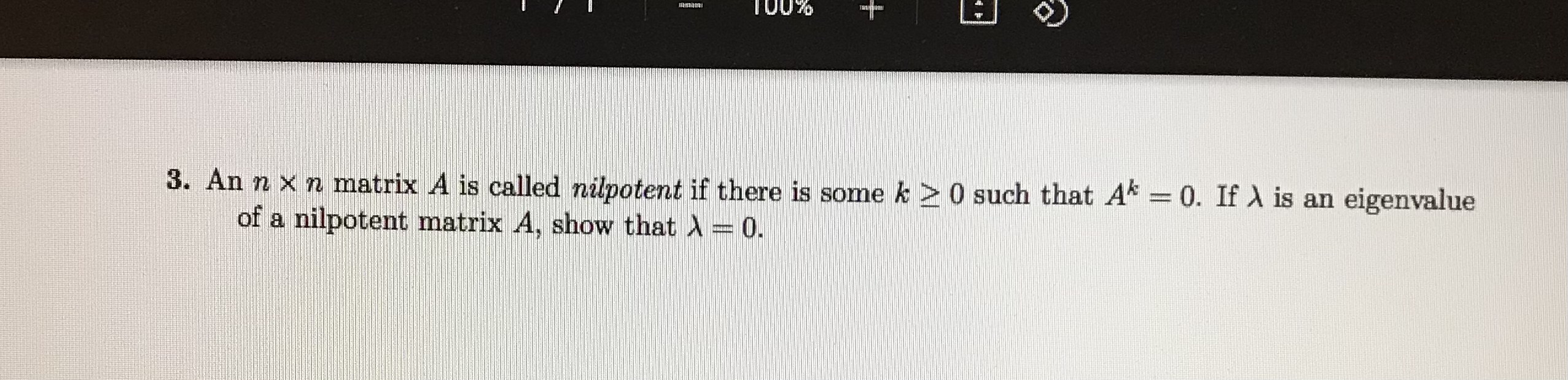
\f3. An n x n matrix A is called nilpotent if there is some k 2 0 such that A* = 0. If ) is an eigenvalue of a nilpotent matrix A, show that A = 0.1. For each of the following matrices A, determine (i) if A is diagonalizable over R and (ii) if A is diagonalizable over C. When A is diagonalizable over C, find the eigenvalues, eigenvectors, and eigenbasis, and an invertible matrix P and diagonal matrix D such that P AP = D. (A) A = 2 2 (B) A = NOOO 0 (C) A = ONE