Question: fA boat is heading towards a lighthouse, whose beacon-light is 10'}r feet above the water. From point A, the boat's crew measures the angle of
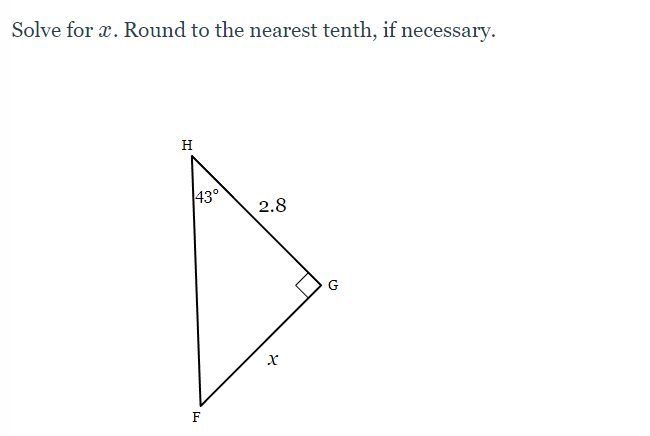

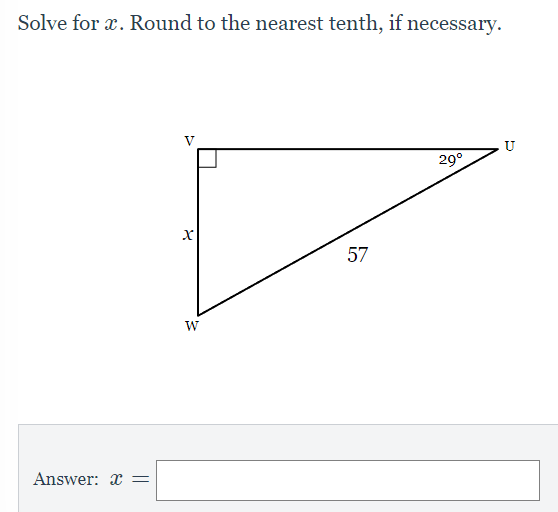
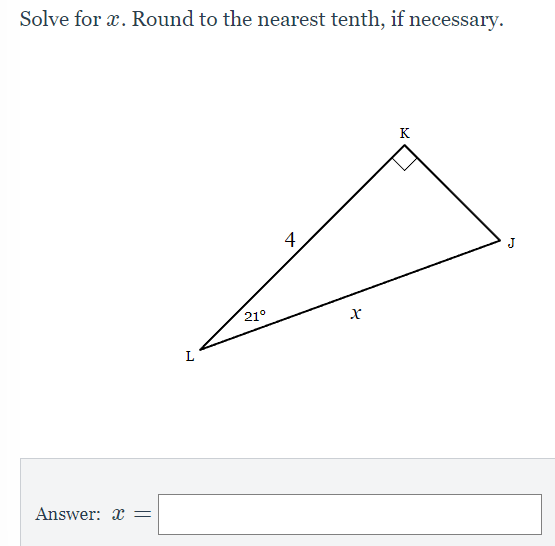
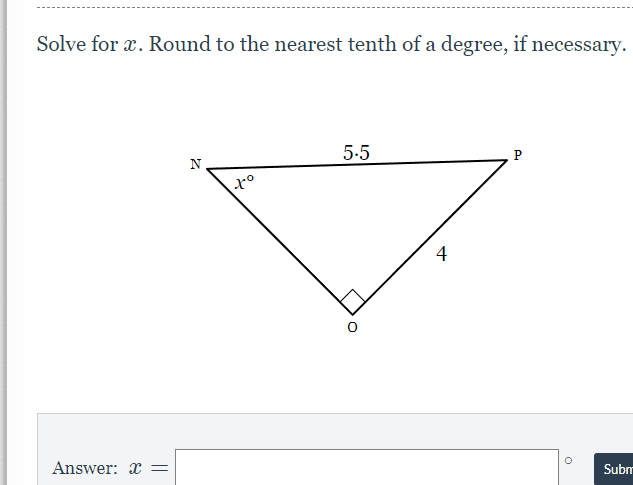



Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


