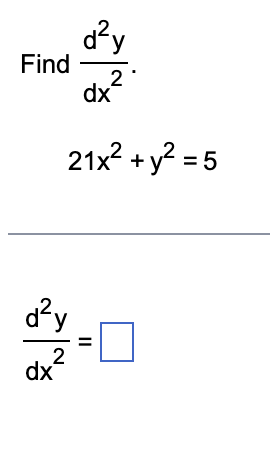
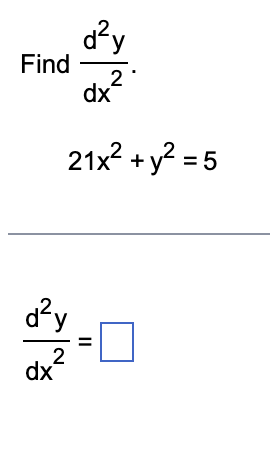
\fa. Verify that the given point lies on the curve. b. Determine an equation of the line tangent to the curve at the given point. 2 2x +xy+4y2=7; (1,1) a. How do you know that the point is on the given curve? The point (1,1) is in the domain of the implicit function. The value of 2x2 + xy+ 4y2 is less than 7 when x is 1 and y is 1. The point (1,1) is in the rst quadrant. The value of 2x2 + xy+ 4y2 is 7 when x is 1 and y is 1. b. Write the equation for the tangent line in slope-intercept form. FD (Use integers or fractions for any numbers in the equation.) differentiating writ n dx yx+ x 94 + + + By dy : 0 Cdx ( x-+sy) : - (Lixty ) dy - (4 x+4) At ( 1, 1 ) dy - ( 4 +1 ) 1+8 - )/9 slope (m ) : -5 9. point ( 1 , 1 ) Equation of tangent is 4- y, : m ( x - x1 ) 4 - 1 : - 2 ( x 7 ) y.: - 51 + 2 7 9 y - 5* + 14. 9 9