Fact: At least one optimal solution -if an optimal solution exists- of a linear program has to be an extreme point (vertex, corner point).

The below figure shows the graphical model of a linear program. The large numbers on the right (1, 2, and 3) indicate the constraints while the small numbers (0, 1, 2, and 3) are the intersection points of the constraints. The feasible region consists of the area to the left of the constraints of 1, 2, and 3 together with x1 ≥ 0 and x2 ≥ 0 constraints.

Three objective functions are under consideration as indicated by three lines labeled A, B, and C. The arrows represent the directions of increasing

objective function value. Objective B is parallel to constraint 3.

In each of the below cases, specify the location of the optimal solution. If there is more than one optimal solution, characterize all of them and also indicate which of these solutions the simplex algorithm can find.

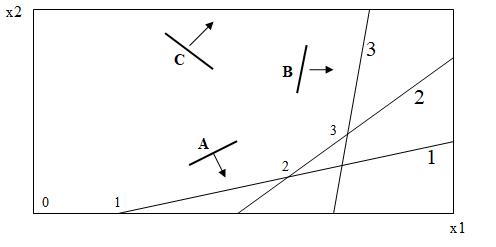
1. Maximize A.
2. Maximize B.
3. Maximize C.
4. Minimize A.
5. Minimize B.
6. Minimize C.
7. Drop x1 ≥ 0 and minimize C.

Transcribed Image Text:

x2 3 B 3 1 1 х1 x2 3 B 3 1 1 х1

Answer rating: 100% (QA)

Concepts that we will use Step 1 Since the objective function is Z ax by draw a dotted line for the equation ax by k w k is any constant Sometimes it ... View the full answer