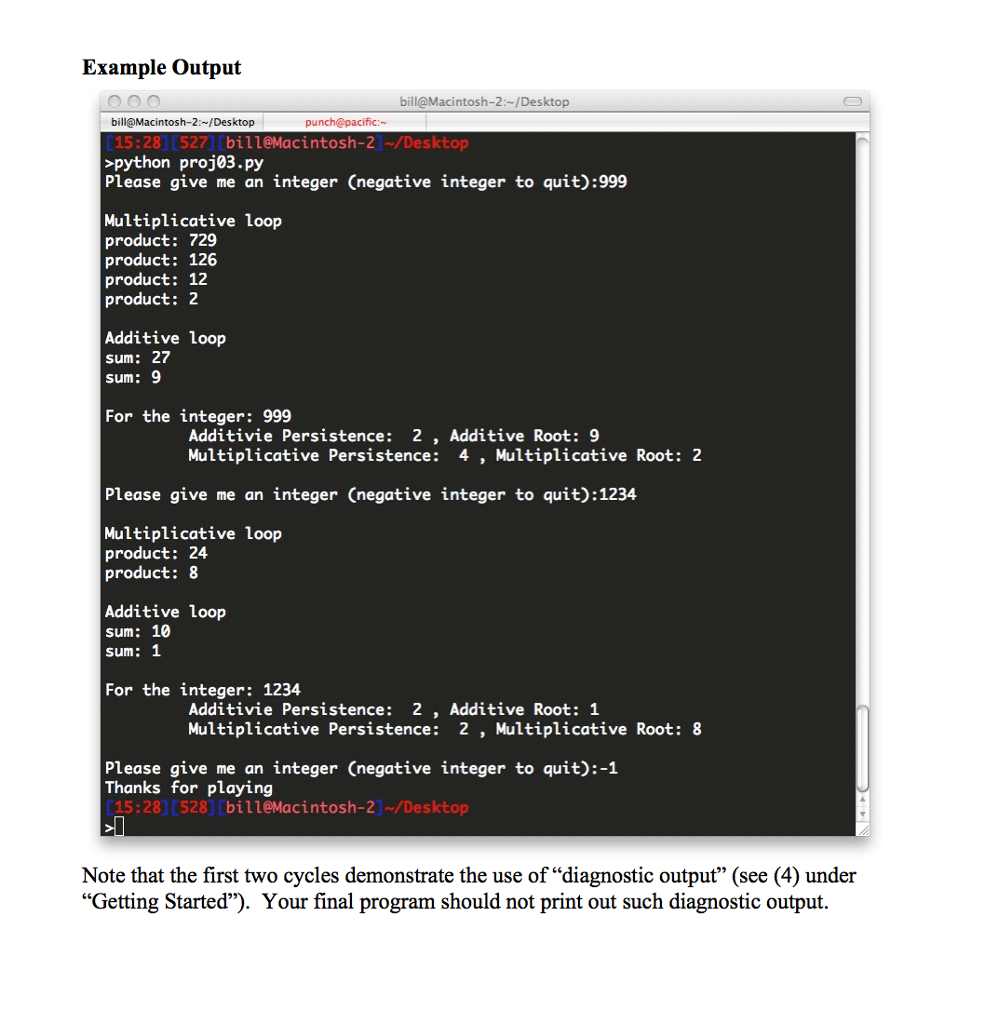
Fall '17 Programming Project 1 Assignment Overview The aim of this project is practice the use of while loops and conditionals statements. You are going to write a program that prompts the user for an integer and then determines the additive persistence and corresponding additive root, and the multiplicative persistence, the corresponding multiplicative digital root of that integer. You will continue to do so until the user quits Background There are many properties of numbers that one can investigate. The ancient Greeks were fascinated with the properties of integers, even ascribing them mystical properties One such property is an integer's additive persistence and its resulting additive root (http://mathworld.wolfram.com/AdditivePersistence.html). Additive persistence is a property of the sum of the digits of an integer. The sum of the digits is found, and then the summation of digits is performed on the sum, repeating until a single integer digit is reached. The number of such cycles is that integer's additive persistence. Consider the following example 1. The beginning integer is 1234 2. Sum its digits is 1+2+3+4-10 3. The integer is now 10 4. The sum of its digits is 1 +0 1 5. The integer is 1. When the value reaches a single digit, we are finished. This final integer is the additive root The number of cycles is the additive persistence. The integer 1234 has an additive persistence of 2 (first sum was 10, then the second sum was 1). The final digit reached is called the integer's additive digital root. The additive digital root of 1234 is1. The multiplicative persistence http://mathworld.wolfram.com/MultiplicativePersistence.html) and resulting multiplicative root are determined the same way, only multiplying the digits of an integer instead of adding. For example 1. 2. 3. 4. 5. The beginning integer is 1234 The product of 1*2*3*4 = 24 The integer is now 24 The product of 2*4 8 The integer is now 8. When the value reaches a single digit, we are finished. This final integer is the multiplicative root