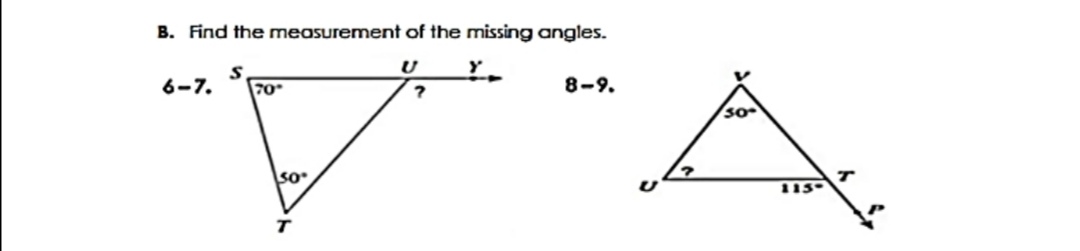
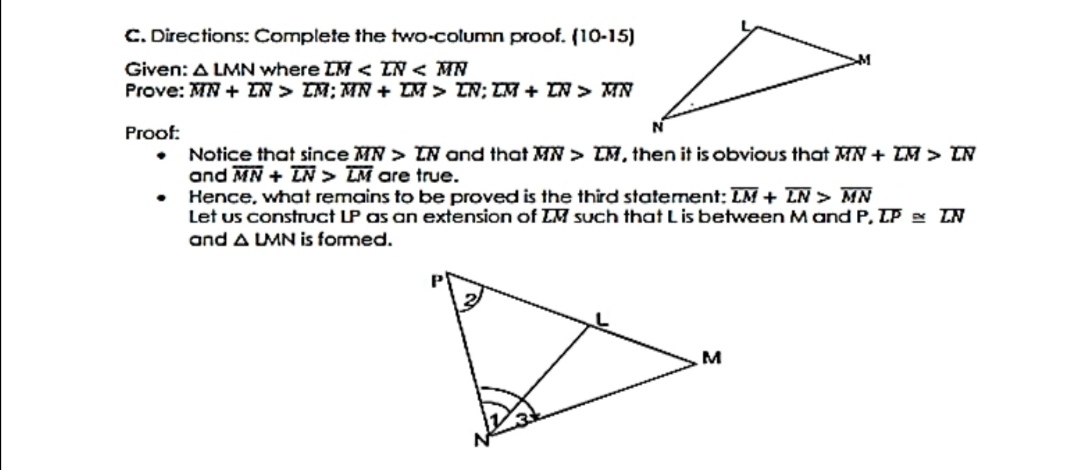
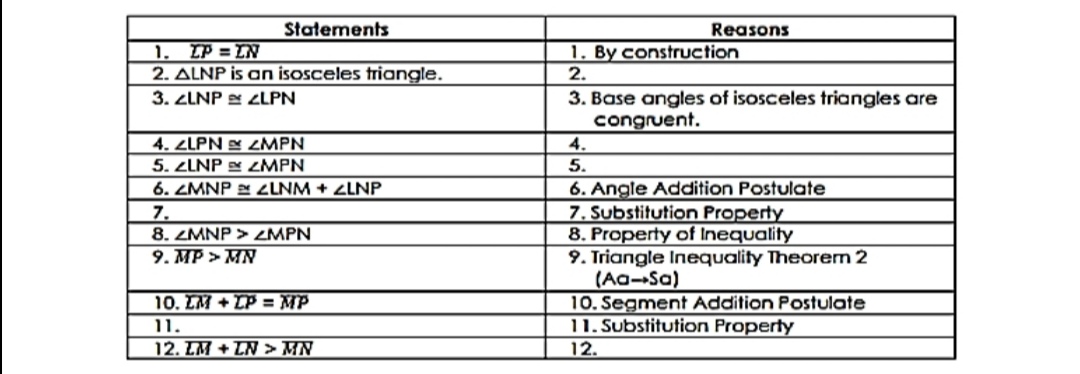
Question: fC. Directions: Complete the two-column proof. (10-15) Given: A LMN where IM ZM; MN + LM > IN; ZM + IN > MIN Proof: Notice
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


