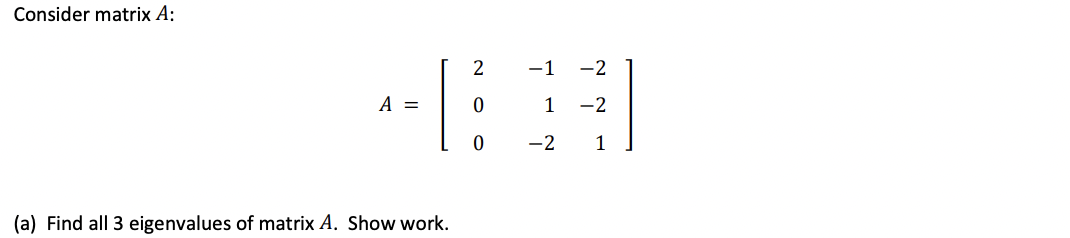
\f(c) Find all 3 eigenspaces of matrix A. Show work (Note: You should be able to evaluate the determinant by hand without using matlab's roots function) Stipulation: To show work, you must set up the necessary nullspace equations (A - An1 ) v = 0, and also, write out all the row reduction steps that lead towards the answers for each eigenvector of A. (d) Now, you can actually check your row-reduction work in matlab !! In your matlab script, add the 3 following commands and echo the answers for each. Ideally, if your math in (c) were all correct, the RREF answers from these 3 commands will help you verify the correct "free column" positions for your work in (c). rref work for v1A rref (A - D(1, 1) *eye (3) ) These 3 commands are equivalent to this rref work for v2A rref (A - D (2, 2) *eye (3) ) expression: rref work for v3A = rref (A - D(3, 3) *eye (3) ) rref ( A - An I) where "D" = the eigenvalue matrix from your eig command: [V, D] = eig (A)(e) Compare your hand-derived eigenvectors versus the answer from the eig command: From the eig command Hand-derived eigenvectors (or eigenspaces) 0.xxxx 0. xxxx V OOH 0. xxxx 0. xxxx 1, = s :, vz = t [: ] , v. = w : -0.xxxx 0. xxxx V2 V3 whole number entries for all 3 vectors, where s, t, and w are arbitrary constants (decimal entries) Find the unit vector versions of V] , V2 , and V3 by hand, and show they do match up with the eigenvector answers from the eig command. (f) Take a look at your 3 eigenvectors v1 , V2 , and v3 again. Do they form a linearly-independent set ? Explain your results by using matlab's rref command, and add the following to your matlab script: Echo any rref results that could help you ascertain whether v1 , v2 , and 13 are linearly independent or not Using the disp command, type out your reasonings and echo it. For instance, you can write: disp ('I think v1, v2, v3 from matrix A are linearly independent because ... ' ) g) Using your answers from (f), answer this question: Does the inverse of the eigenvector matrix V exists ? Justify your answers in 1 or 2 sentences. (h) Moral of the story for Problem 1: Fill in the blanks for the following sentenceWhen matrix A possesses 3 distinct eigenvalues, the eigenvectors of A are linearly - As a result, the eigenvector matrix V is (invertible or not invertible - choose one) (independent or dependent - choose one)