Feedback

1. The objective function can be expressed mathematically by multiplying the unit contribution margin by the units to be produced for each product and then summing over all products. An internal constraint is a limiting factor found within the firm. External constraints are limiting factors imposed on the firm from external sources. Nonnegativity constraints simply reflect the reality that negative quantities cannot be produced and are usually included in the constraint set. Constraints are expressed as inequalities, where the amount of scarce resource used per unit of product is multiplied by the units to be produced for each product and summed. This is compared to the amount of the resource available.

2. Four steps are followed in solving the problem graphically:

1. Graph each constraint.
2. Identify the feasible set of solutions. A feasible solution is one that satisfies the constraints in the linear programming model. In this case, look for the inmost shape on the graph.
3. Identify all corner-point values in the feasible set. Corner points are the corners of the area on the graph that satisfies the constraints. You may have to use algebra to solve simultaneous equations to pinpoint where two of the constraint lines meet.
4. Select the corner point that yields the largest value for the objective function. Plug the x and y values for each corner point into the objective equation. Which one results in the highest value?

3. A binding constraint is one whose limited resources are fully used by a product mix. Plug the x and y values for the point that yields the largest value for the objective function into the internal constraint equations and determine which constraint is met.

A loose constraint is one whose limited resources are not fully used by a product mix.

An internal constraint is a limiting factor found within the firm. External constraints are limiting factors imposed on the firm from external sources.

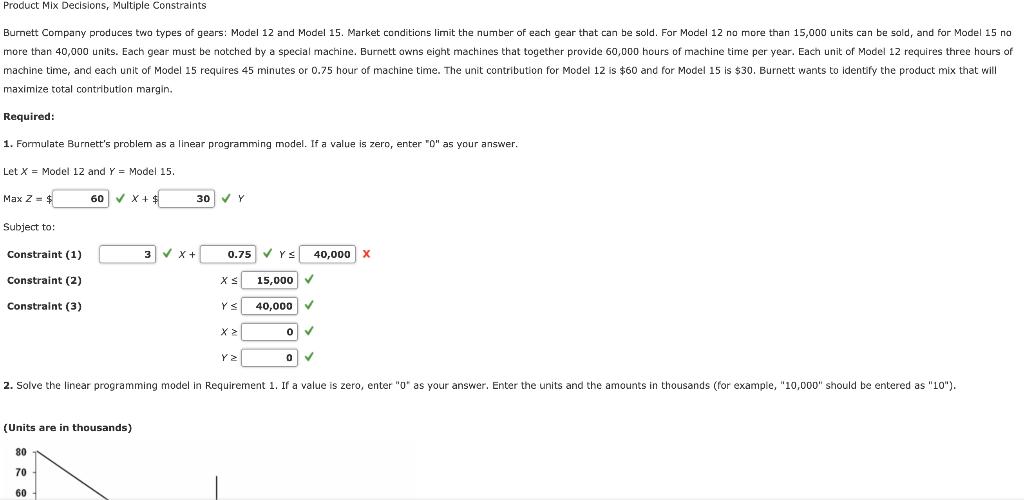
Product Mix Decisions, Multiple Constraints Burnett Company produces two types of gears: Model 12 and Model 15. Market conditions limit the number of each gear that can be sold. For Model 12 no more than 15,000 units can be sold, and for Model 15 no more than 40,000 units. Each gear must be notched by a special machine. Burnett owns eight machines that together provide 60,000 hours of machine time per year. Each unit of Model 12 requires three hours of machine time, and each unit of Model 15 requires 45 minutes or 0.75 hour of machine time. The unit contribution for Model 12 is $60 and for Model 15 is $30. Burnett wants to identify the product mix that will maximize total contribution margin.. Required: 1. Formulate Burnett's problem as a linear programming model. If a value is zero, enter "0" as your answer. Let X = Model 12 and Y= Model 15. Max Z = $ Subject to: Constraint (1) Constraint (2) Constraint (3) 60 X + $ 30 Y (Units are in thousands) 80 70 60 3x+ 0.75 YS 40,000 X X Y YZ 15,000 40,000 0 2. Solve the linear programming model in Requirement 1. If a value is zero, enter "0" as your answer. Enter the units and the amounts in thousands (for example, "10,000" should be entered as "10").