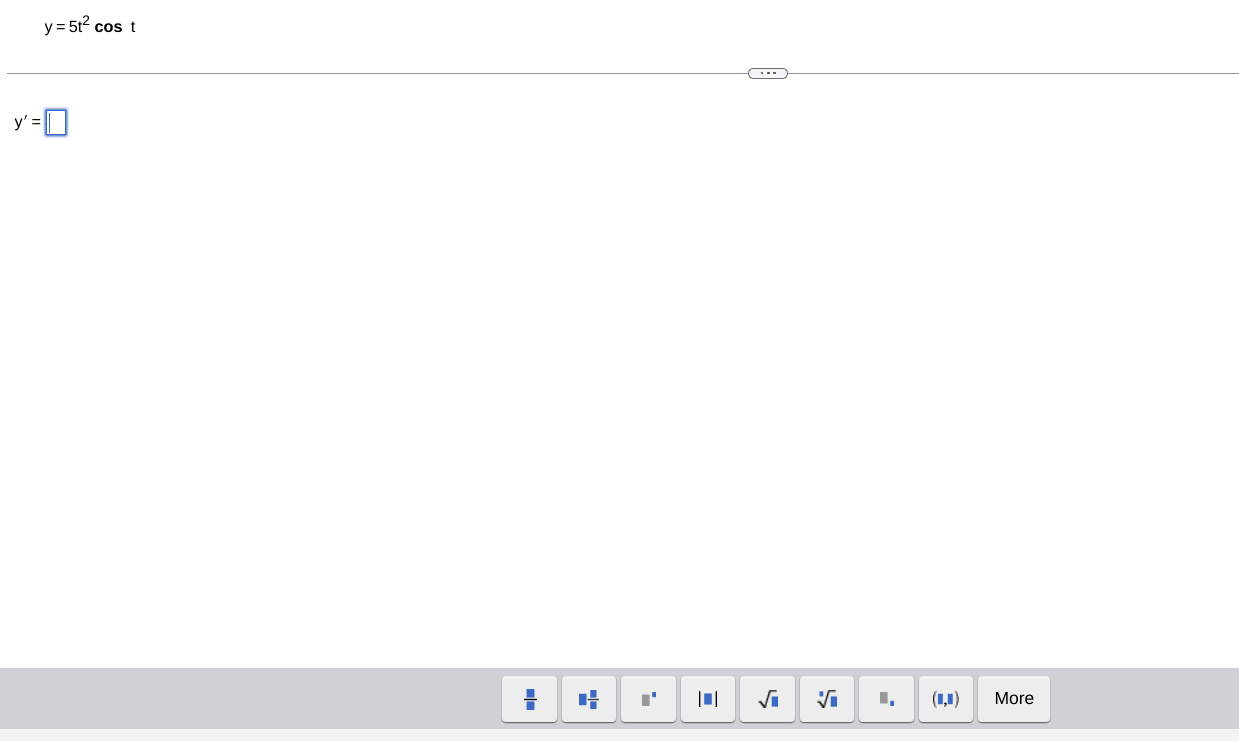
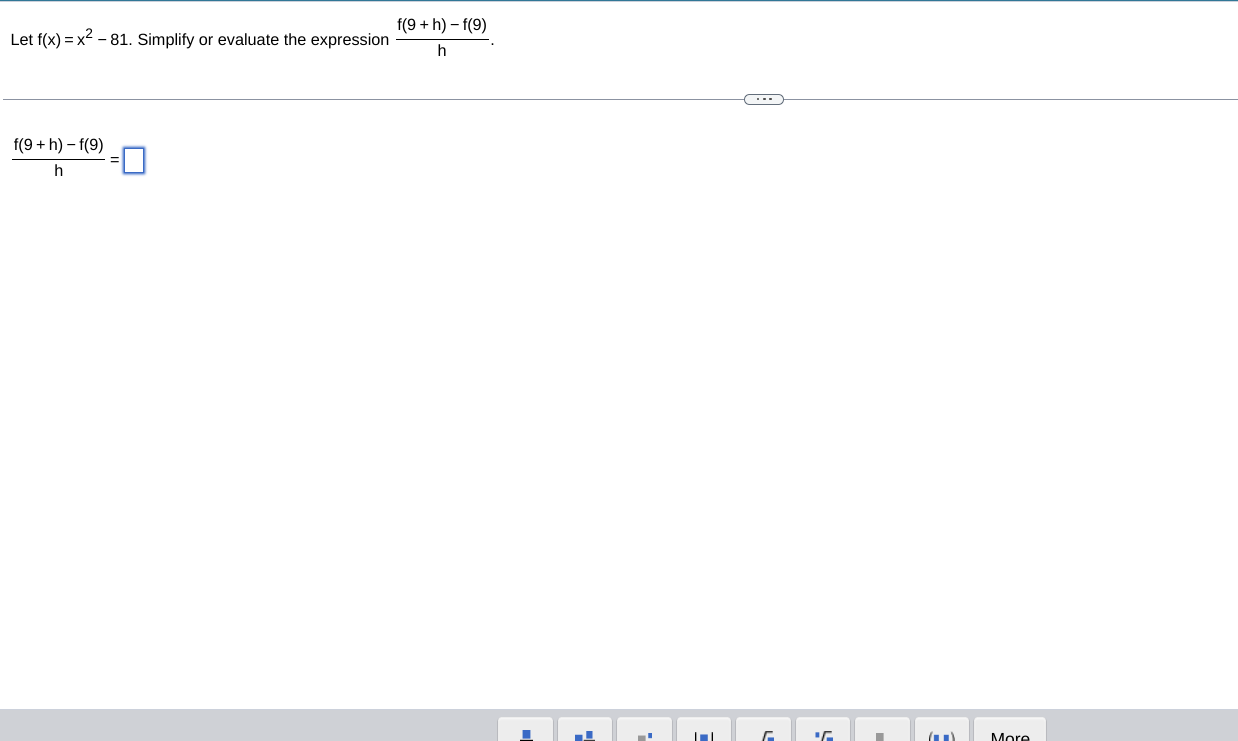
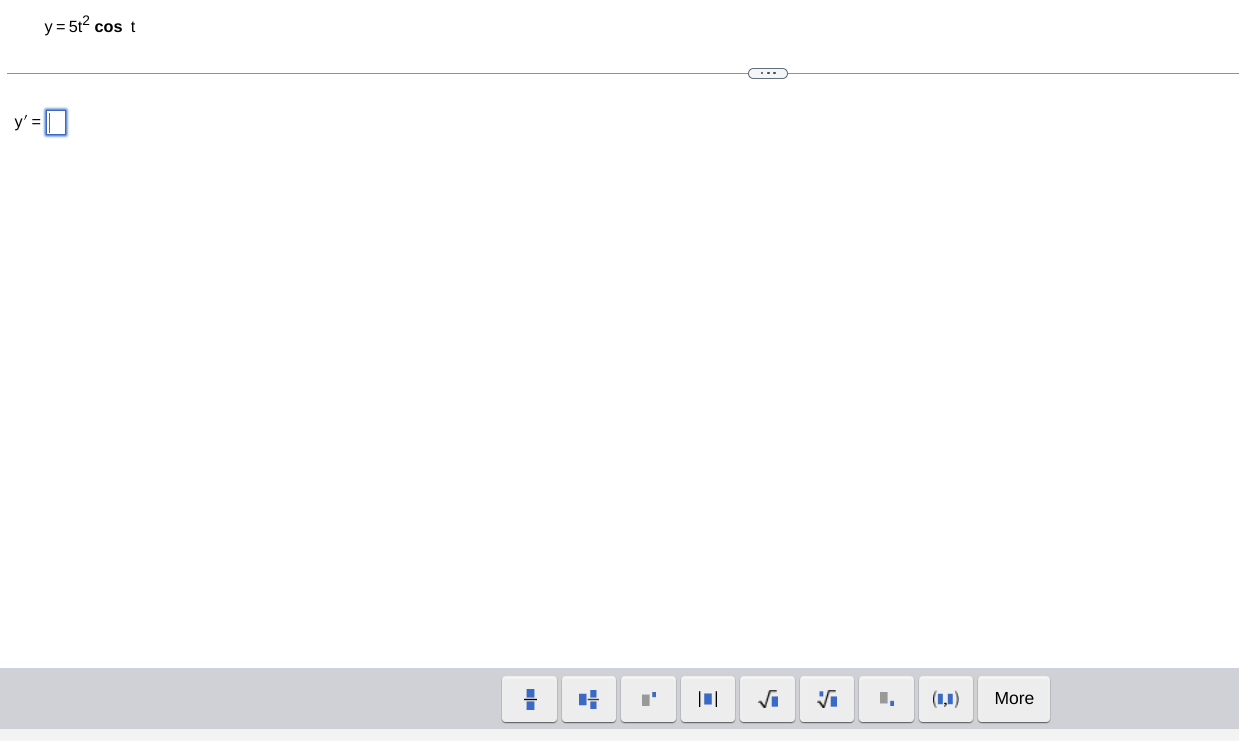
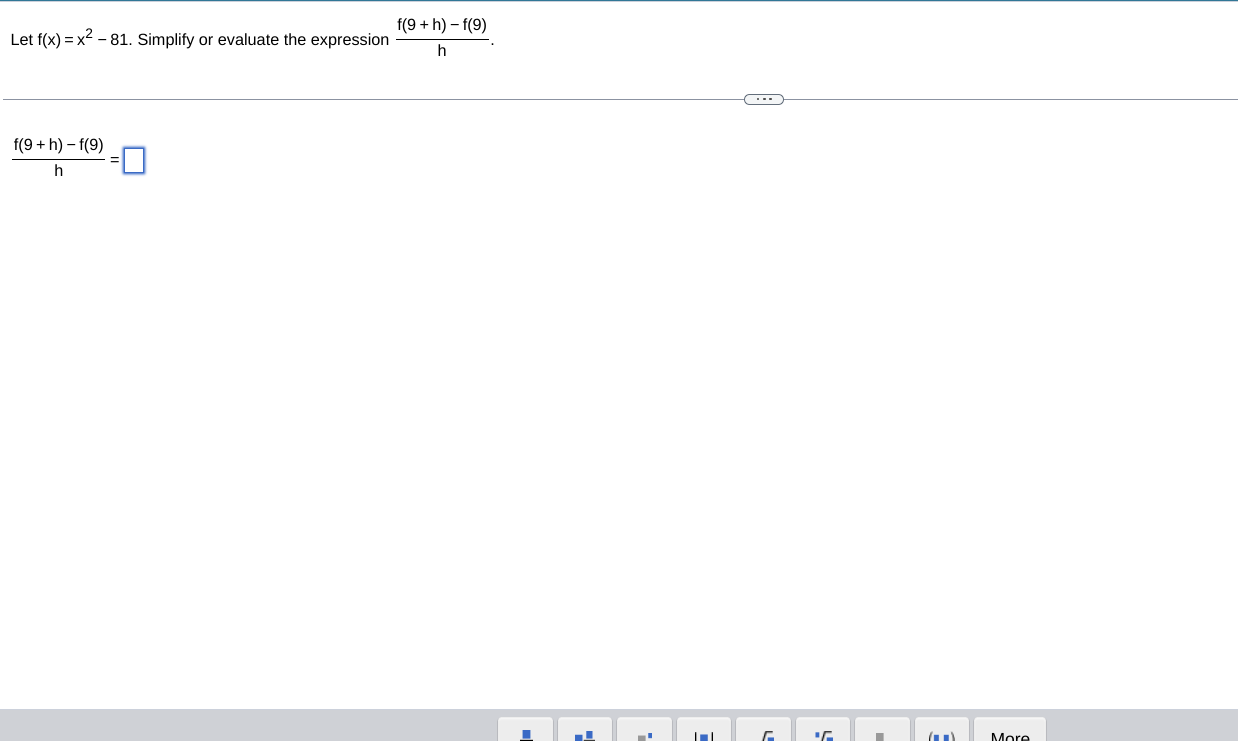
\fEvaluate the derivative of the function. y = sec - (2 In 4x) To find 1 du dx ' let u = 2 In 4x and use the derivative formula - (sec - lu) = |uvu2 -1 dx du d Use the Chain Rule to find - = = dy (2 In 4x). dx (2 In 4x) = du Replace u and dx - with the terms found in previous steps in the formula for the derivative. 1 du 1 XIN |ulduz-1 dx |2 In 4x| (2 In 4x) 2 - 1 2 x/2 In 4x| (2 In 4x) 2 - 1 2 Therefore, -(sec - 1(2 In 4x)) = x/2 In 4x| (2 In 4x) 2 - 1 Print Close