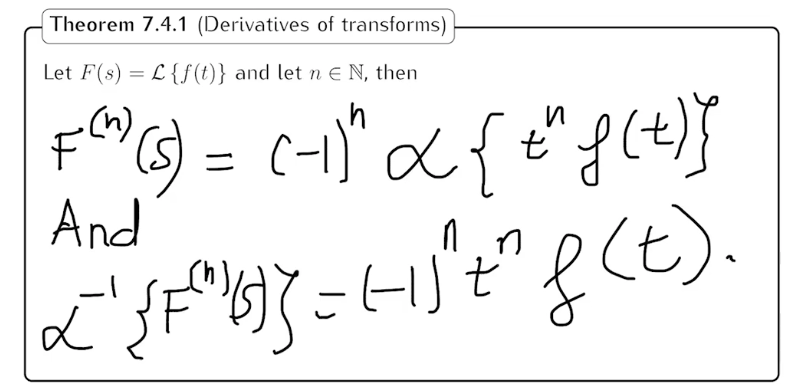
\fExercise 1: Use theorem 7.4.1 to compute C {t sin(2() }. Exercise 2: Write the following inverse Laplace transforms as convolutions (Write them as inte- grals, but you don't have to evaluate the integral): 1 . C-13 ($2 (8 + 1 ) ] 2. [ (s' + 4 ) (82 + 1 ) ) S Exercise 3: Consider the following ODE: y" (t ) + 4y(t) = f(t), y(0) = a, y'(0) =b. where f is some function that you don't know. 1. Apply LT to the ODE and solve for Y(s). Your solution would look like Y(s) = H(s) F(s) + I(s), where F(s) = C{f(t)}. 2. Apply the ILT to Y(s). Part of your solution may be involve an integral. Story: We managed to write y(t) in terms of a, b and f. The integral in y(t) might look scary but we have some very accurate and fast methods to compute integrals. This expression allows us to quickly jump from a given f(t) to the solution y(t). The function H is called a transfer function. Let me know if you want to learn more about numerical integration or about transfer functions. Exercise 4: Use Laplace transform to the following (so called integro-differential equation) to find y(t) y'(t) = 1 - sin(t) - / y(r) dr, y(0) =0. Note: The steps are similar the ones for ODES: Apply LT, solve for Y(s), apply ILT