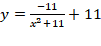
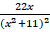
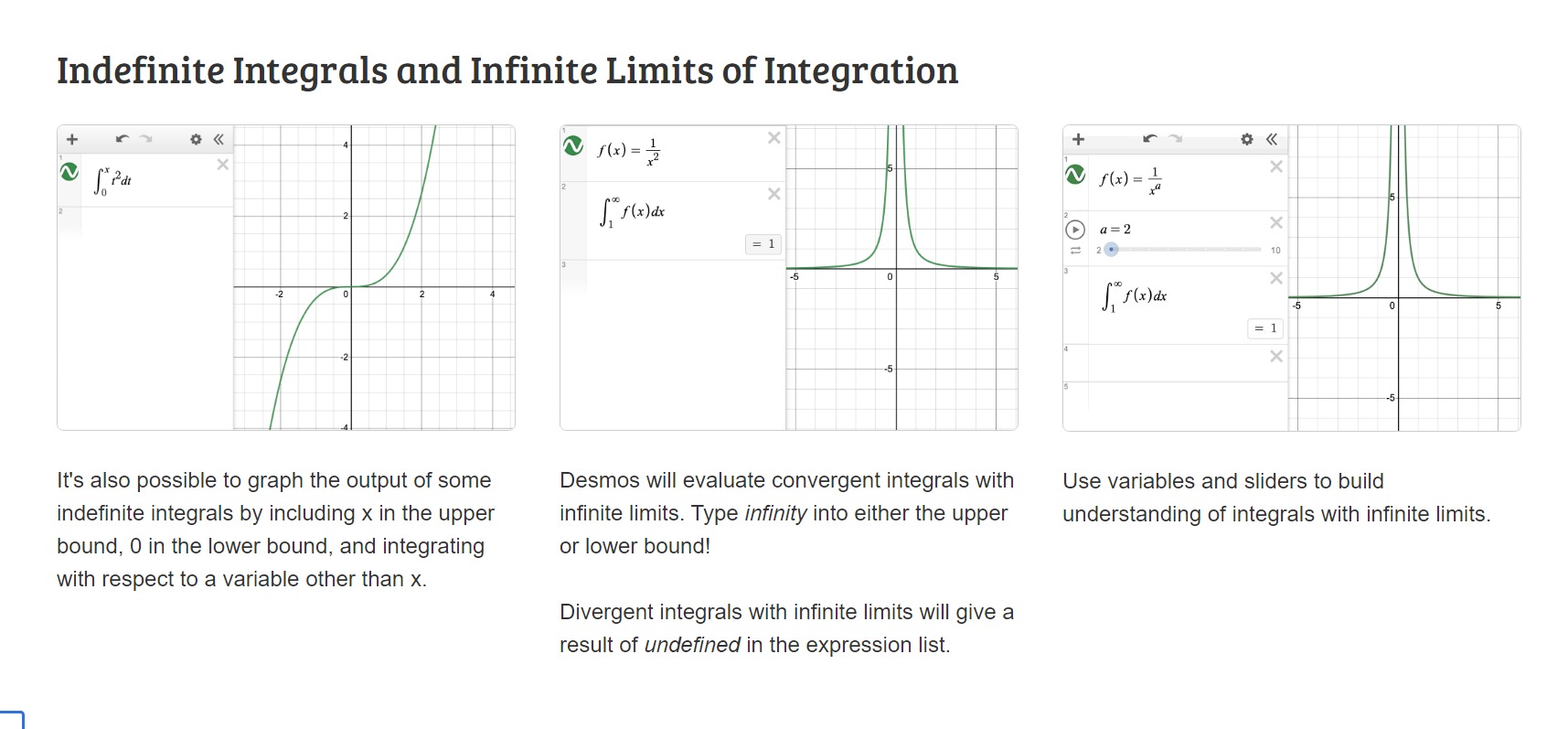
\f\f2. In Desmos, graph the derivative function from your application problem in Discussion &. Then graph its antiderivative so that the maximum value of the antiderivative function is twice as great the maximum value of your function 2c from Discussion 1. 3. Using the graph of antiderivative function estimate the y-intercept and the end value of the function (as x 4-o0). 4. Interpret the y-intercept and the end behavior of the antiderivative function in the context of your application problem. There are multiple due dates in this assignment. Remember to use the Canvas Equation Editor. Refer to the Tools for Mathematics page in the Course Specific Information module for technical guidance. Post & Reply o, I Submit the initial post by the end of the 4t day of the module week. Your initial post should include: the graphs of the derivative and antiderivative functions with any necessary graphing elements (notes, points, sliders, etc.) o the estimate and description of the y-intercept and the end behavior of the antiderivative function Indefinite Integrals and Infinite Limits of Integration It's also possible to graph the output of some Desmos will evaluate convergent integrals with indefinite integrals by including x in the upper infinite limits. Type infinity into either the upper bound, 0 in the lower bound, and integrating or lower bound! with respect to a variable other than x. Divergent integrals with infinite limits will give a result of undefined in the expression list. Use variables and sliders to build understanding of integrals with infinite limits