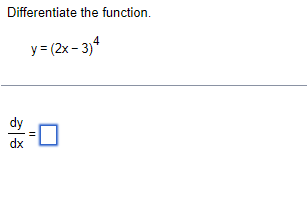
Question: fffDifferentiate the function with respect to the independent variable. 5 f(x) = (4-3x2) 5 f'(x) =Differentiate the function with respect to the independent variable. (1-3x

![variable. (1-3x 2) f(x) = (2-x 2)4 f'(x) =]Differentiate the function below](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/671b7ab50ee51_132671b7ab4c7ef8.jpg)


![animal chews in one minute] is proportional to its body mass raised](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/671b7aba7610f_138671b7aba40d64.jpg)

![some positive constant k. dc [a] Assume that the body mass of](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/671b7abfb523d_143671b7abf8dfd8.jpg)
\f\f\fDifferentiate the function with respect to the independent variable. 5 f(x) = (4-3x2) 5 f'(x) =Differentiate the function with respect to the independent variable. (1-3x 2) f(x) = (2-x 2)4 f'(x) =]Differentiate the function below with respect to N. Assume that t} and It are positive constants. Druzinsky [1993} showed that chewing frequency [i.e.. the number of times an animal chews in one minute] is proportional to its body mass raised to the power of 43.128. that is. if M is the body mass and c the chewing frequency. then c = kM [1.123 for some positive constant k. dc [a] Assume that the body mass of a particular mammal is given by a formula lvlt} = 1 + E. Calculate E' (h) Druzinsky also found that thejaw length of the animal: L. is proportional to its body mass raised to the [1.312 dc power: i.e.. L = rl'rl'312 where r is another positive constant. Calculate dL' the rate of chewing frequency with jaw \fdA Assume that the radius r and the area A = ar of a circle are differentiable functions of t. Express dr dt in terms of dt I. . Choose the correct answer below. dA dr O A. dit dt dr dA O B. = 2xr dit dt dA dr O C. = 2x dt dt dA dr OD. = 2xr- dt dt
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


