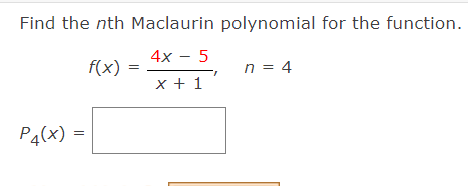
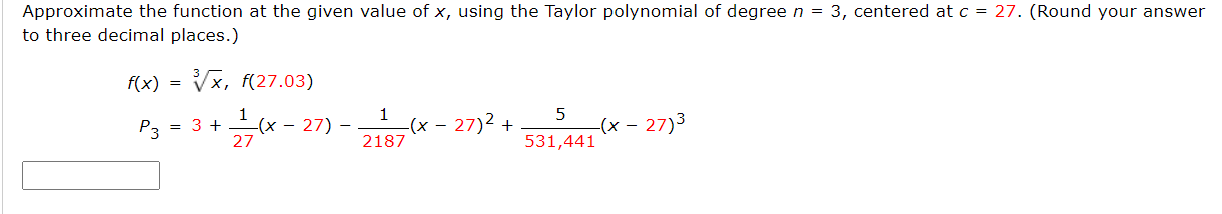
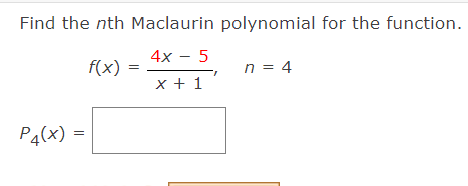
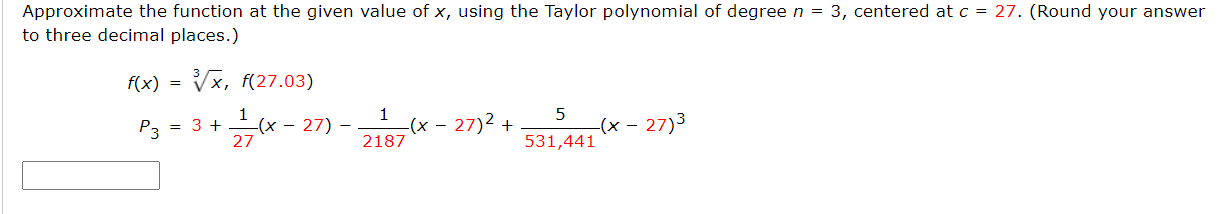
Approximate the function at the given value of K, using the Maclaurin polynomial of degree n = 4. (Round your answer to four decimal places.) Approximate the function at the given value of x, using the Taylor polynomial of degree n = 3, centered at C = 27. (Round your answer to three decimal places.) f(x) = if}, f(27.03) P3 = 3+i(x27) 1 (x27)2+;(x27)3 27 2187 531,441 E Use Taylor's Theorem to obtain an upper bound for the error of the approximation. Then calculate the value of the error. (Round your answers to three significant figures.) (0.5)2 + (0.5)4 2! 4i (305(03):! 1 Determine the degree of the Maclaurin polynomial required for the error in the approximation of the function at the indicated value of x to be less than 0.001. x) = e\Determine the values of x for which the function can be replaced by the Taylor polynomial if the error cannot exceed 0.001. (Enter your answer using interval notation. Round your answer to four decimal places.) 3 f(x) =5inxzxix_ 31