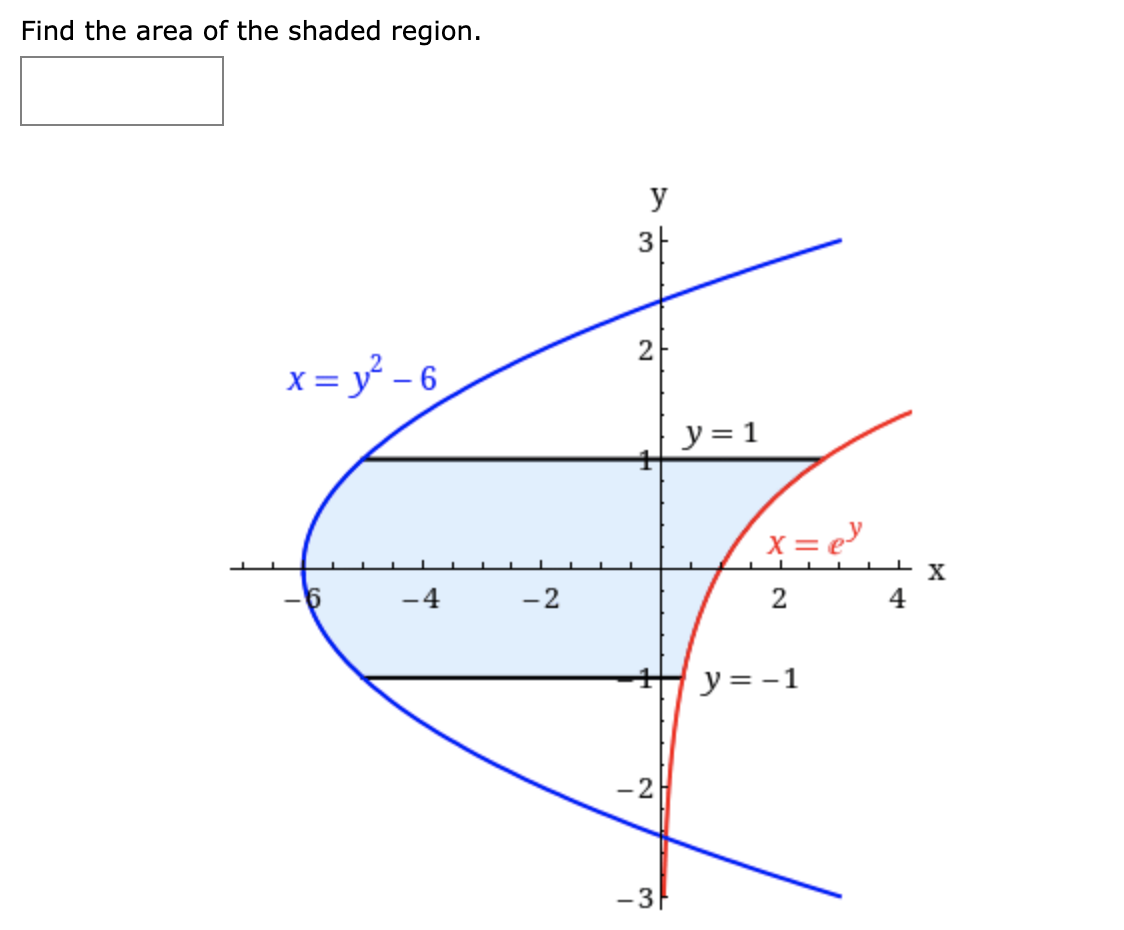
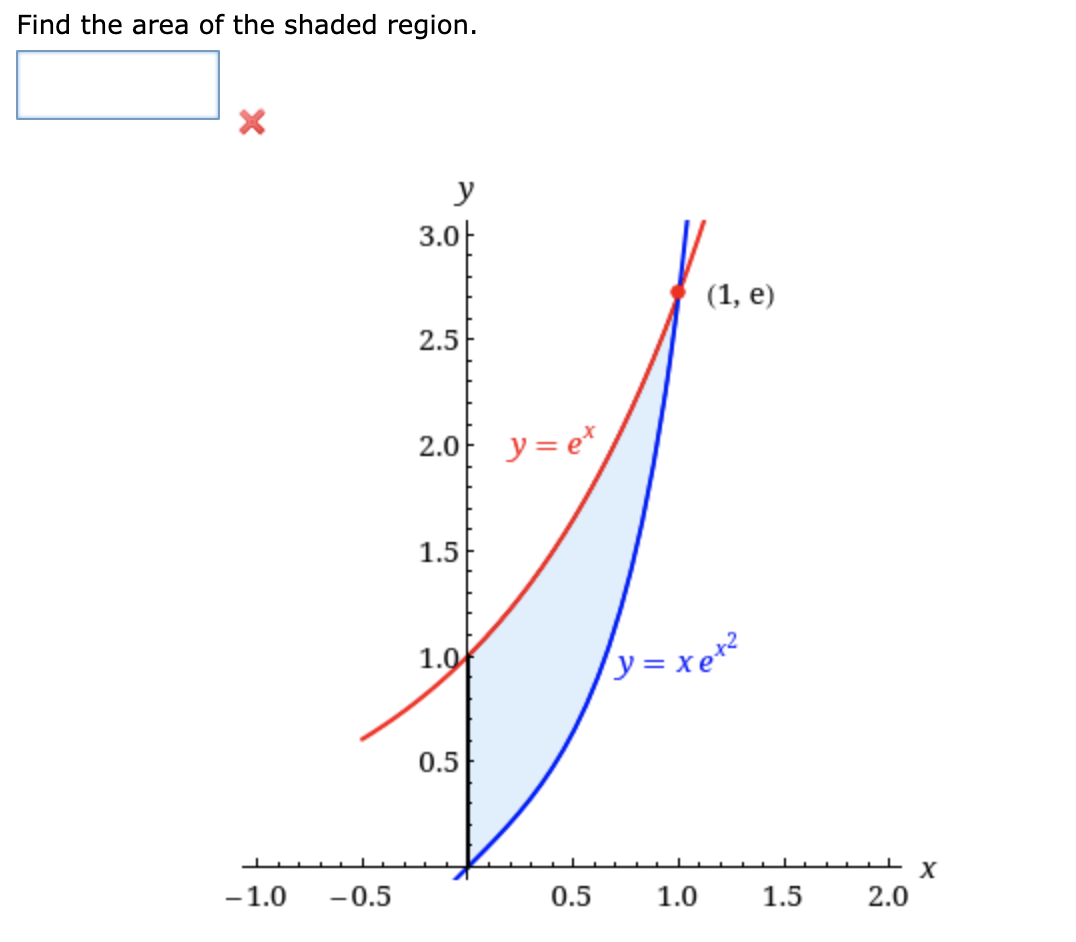
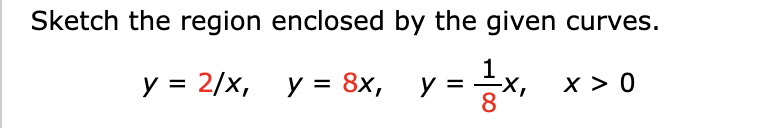Question: fffTutorial Exercise Evaluate the indefinite integral. (In(x)) 47 dx X Step 1 We must decide what to choose for u. If u = f(x), then
\f\f\fTutorial Exercise Evaluate the indefinite integral. (In(x)) 47 dx X Step 1 We must decide what to choose for u. If u = f(x), then du = f'(x) dx, and so it is helpful to look for some expression in (in()_ ax = (In(x))47 -dx for which the derivative is also present, though perhaps missing a X constant factor. For example, In(x) is part of this integral, and the derivative of In(x) is , which is also present.Evaluate the indefinite integral. f cosh/x18) dx X19 We must decide what to choose for u. If u = f(x), then du = f '(x) dx, and so it is helpful to look for some expression for which the derivative is also present, though perhaps missing a constant factor. Il.' cos We can re-write ( x18) dx = cos(i) |:| dx. T x18 X We see that i is part of this integral, and the derivative of i is |:| . X18 X18 _utorial Exercise Evaluate the indefinite integral. 2 f x dx 1+x5 We must decide what to choose for u. If u = ftx), then du = f '(x) dx, and so it is helpful to look for some . . x2 expression In 5 1 + x dx for which the derivative is also present, though perhaps missing a constant factor. Finding u in this integral is a little trickier than in some others. We see that 1 + X6 is part of this integral, but the derivative of 1 + X6 is |:| , which is not present in the integrand. However, notice that the x2 in the numerator is close to the derivative of x3, which is |:| . \f
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts