Question: ffQ3 (3 points) Use the given zero (root) x = 33' to find all zeroes of the polynomial function p(x) = x3 + x:2 +
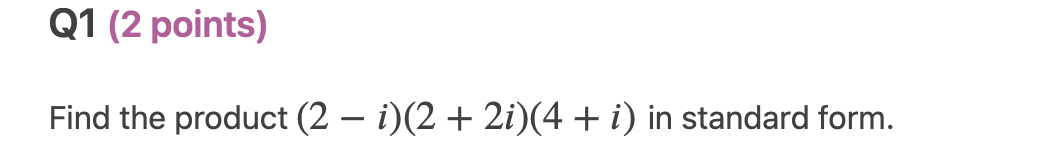

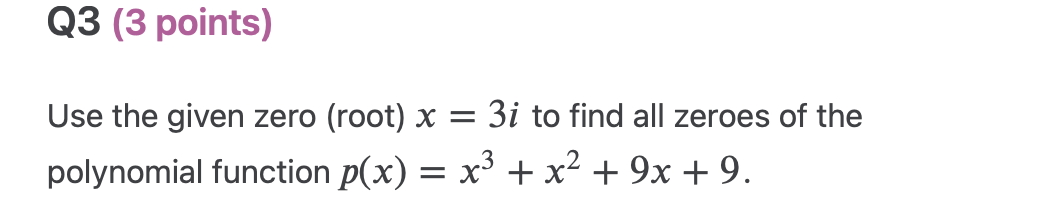

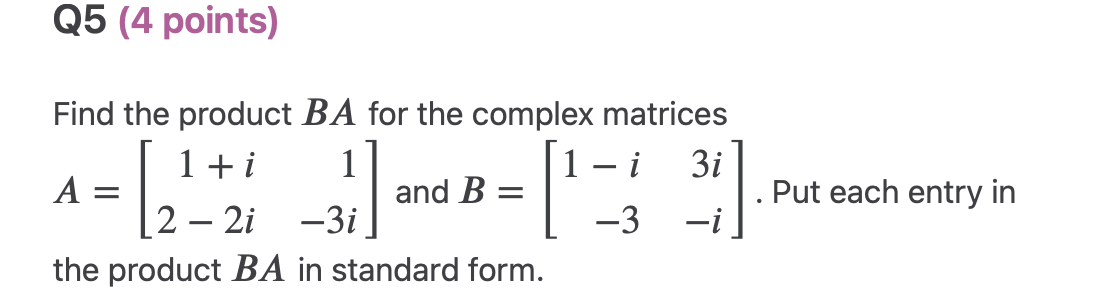
![1 1 i 31' and B = [ ] . Put each](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6703ef597f4fe_1296703ef5962e41.jpg)
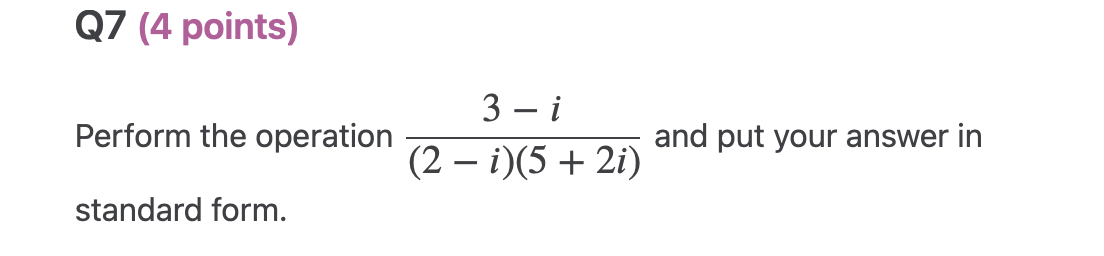
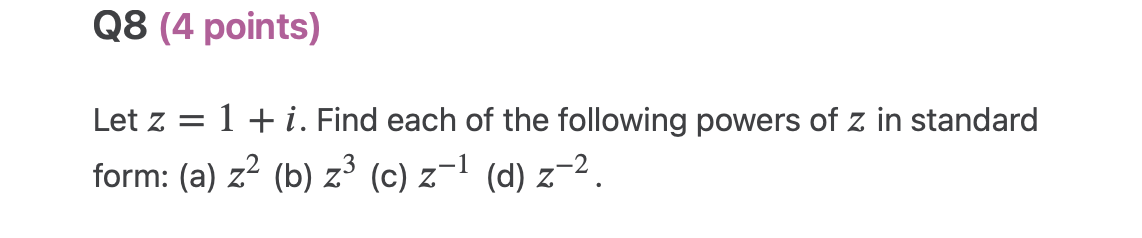
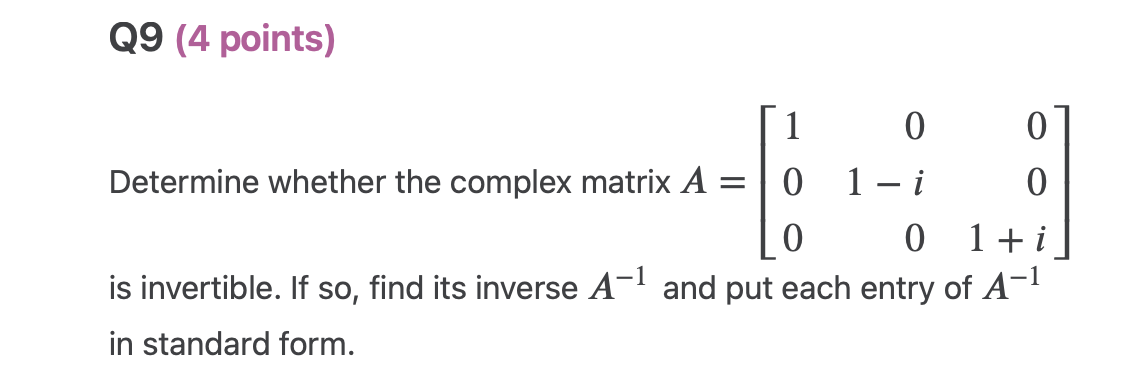
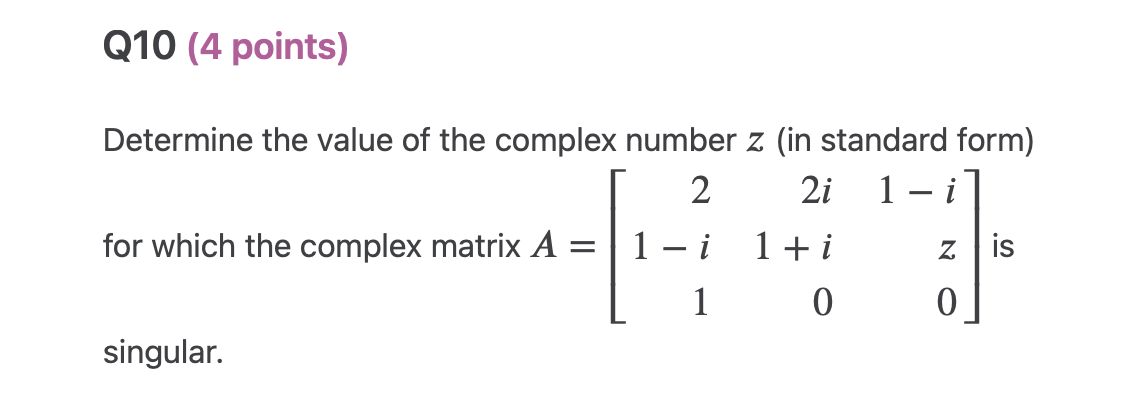
\f\fQ3 (3 points) Use the given zero (root) x = 33' to find all zeroes of the polynomial function p(x) = x3 + x:2 + 9x + 9. Q4 (3 points) 1 - i 3i Find the determinant of the complex matrix B = -3 -i05 (4 points) Find the product BA for the complex matrices 1 + i 1 1 i 31' and B = [ ] . Put each entry in 2 2i 3i 3 i the product BA in standard form. A: Q6 (2 points) Let z = 2 + i and v = -5i. Find the modulus | zu2|.Q7 (4 points) 313 (2i)(5 +2i) Perform the operation and put your answer in standard form. QB (4 points) Let z = 1 + 3'. Find each of the following powers of z in standard form: (a) 22 (b) 23 (c) 21 (d) 22. 09 (4 points) 1 0 0 Determine whether the complex matrix A = 0 1 i 0 0 0 1 + i is invertible. If so, find its inverse A1 and put each entry of A1 in standard form. Q10 (4 points) Determine the value of the complex number 2 (in standard form) 2 2i 1 i for which the complex matrix A = 1 i 1 + i z is 1 0 0 singular
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


