Question: Which expression equals log A for any A > 0 and B > 0? B O a. A log (B) O b. log(A) - log(




![:r: : 3:4 to m : :35 (overthe intervals [0, 3:2] and](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66662b6191712_80966662b6180f9d.jpg)
![[$4, 315]). O b. From :1: : 3:2 to m : 3:4](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66662b61d9d13_80966662b61be145.jpg)
![(over the interval [322, 3:4]; 0 c. From :1: : 0 to](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66662b6231e09_81066662b621f2fa.jpg)
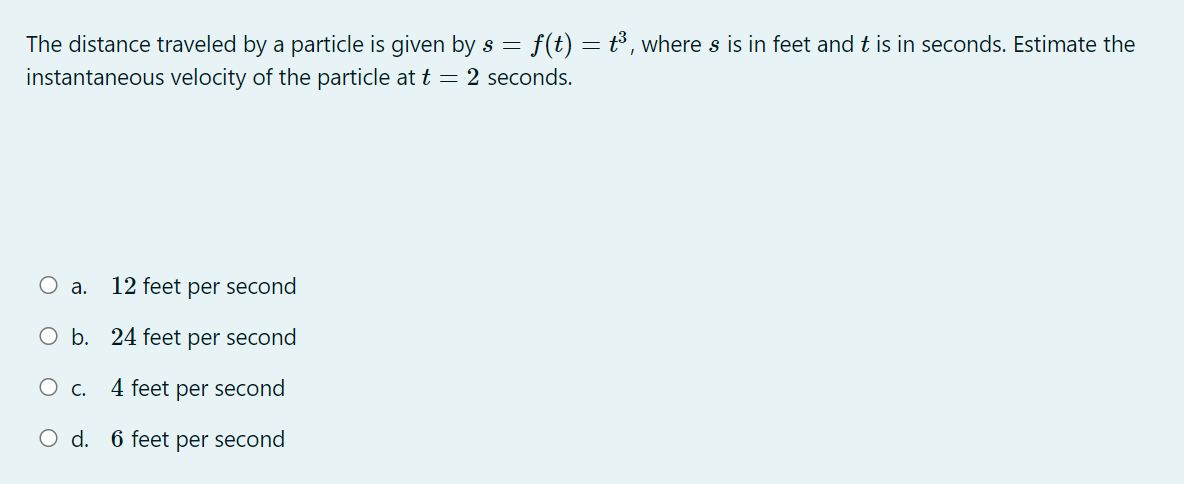
![(overthe intervals [0, 3:1] and [$3, 315]). 0 cl. From :1: :](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66662b62b46c4_81066662b62a2405.jpg)
![$1 to m : 3:3 (over the interval [321, 33]}. At which](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66662b6305f2b_81066662b62e7392.jpg)


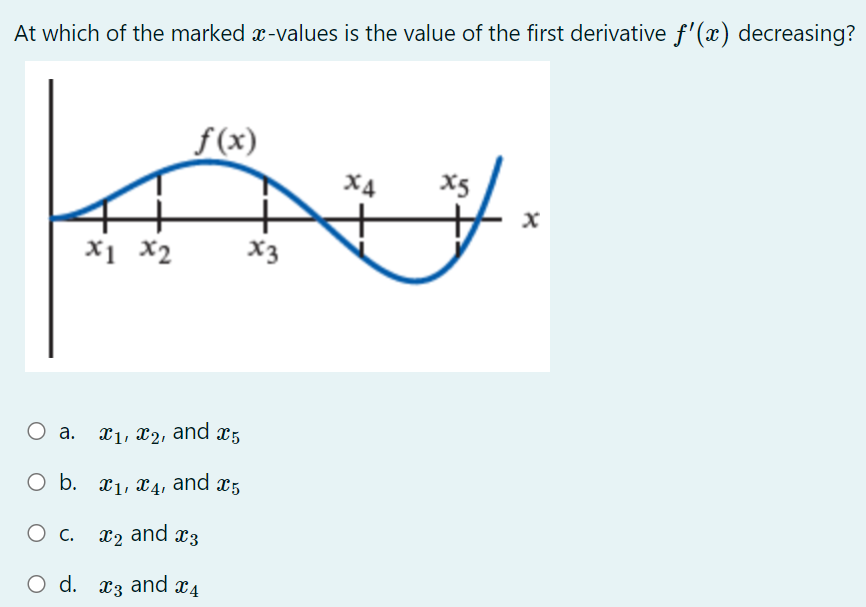
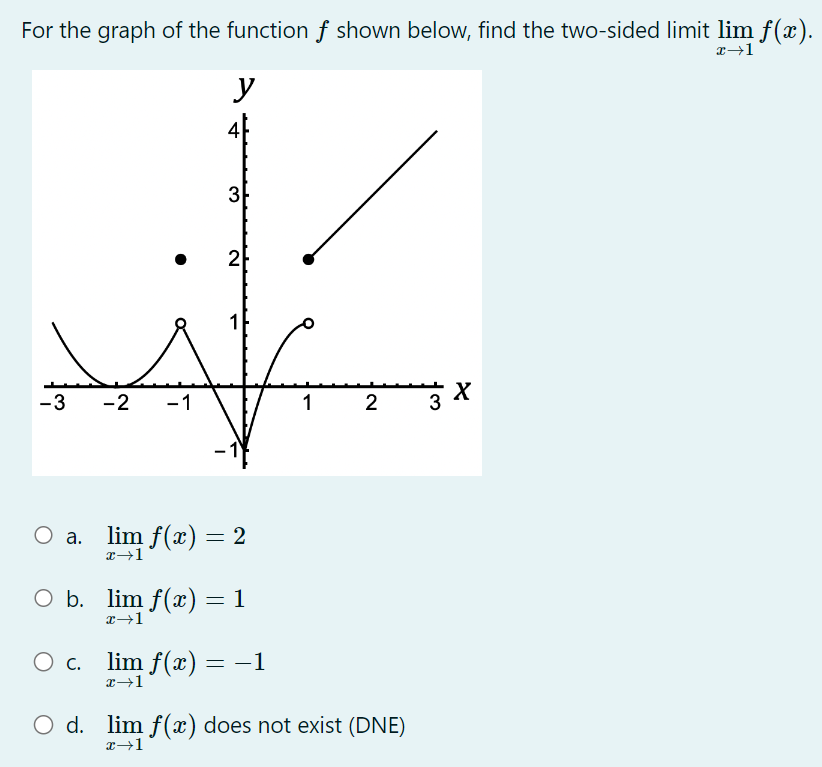

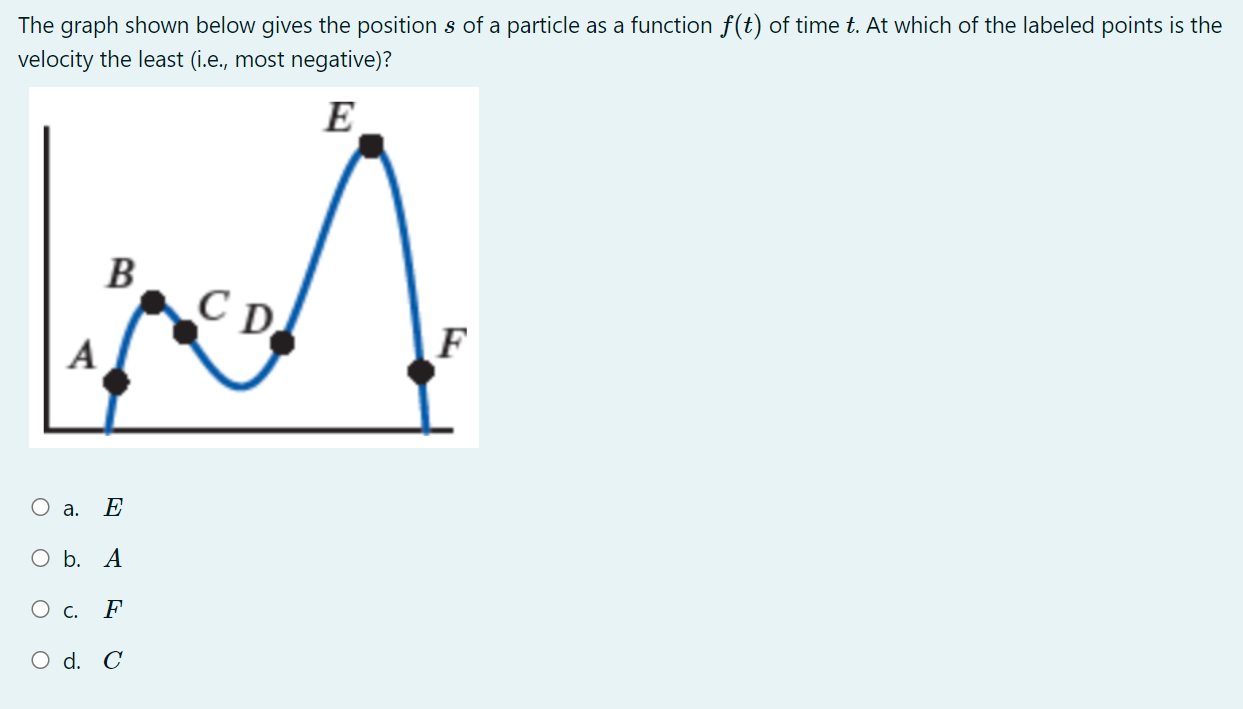

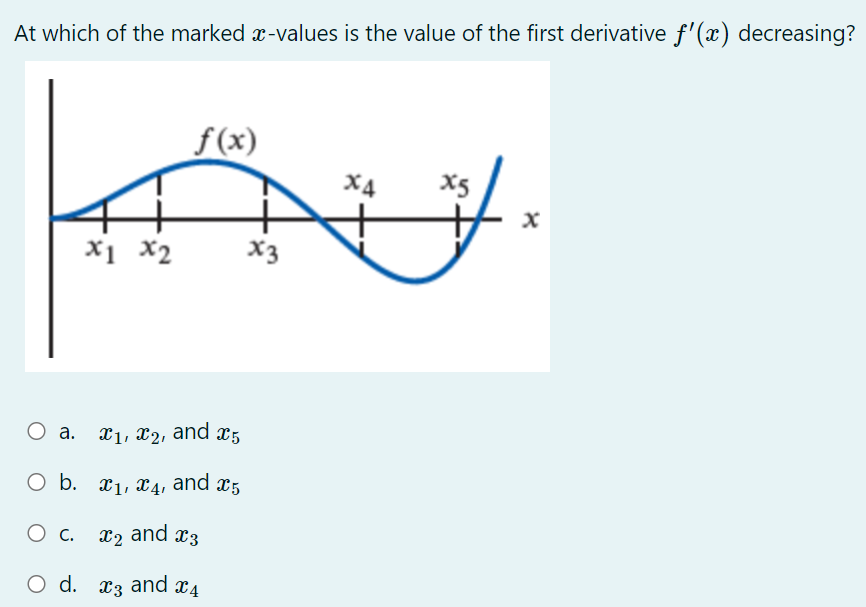
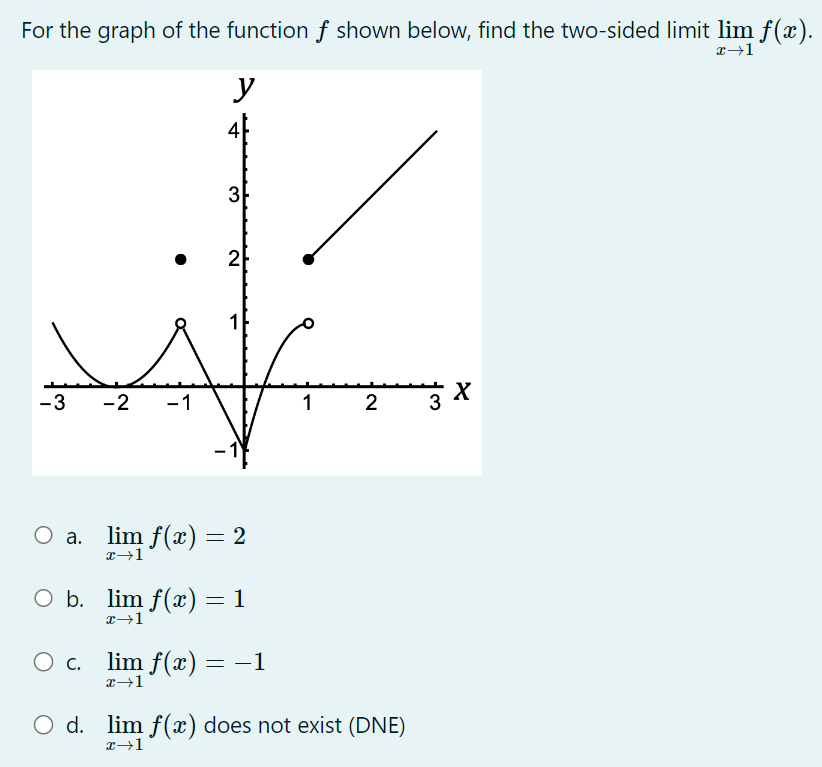
Which expression equals log A for any A > 0 and B > 0? B O a. A log (B) O b. log(A) - log( B) O c. log(A - B) O d. log (A) log (B)The graph shown below is the graph of the derivative 3\" of some function f. On which interval{s) is the function f decreasing? O a. From :1: : 0 to :1: : 3:2 and from :r: : 3:4 to m : :35 (overthe intervals [0, 3:2] and [$4, 315]). O b. From :1: : 3:2 to m : 3:4 (over the interval [322, 3:4]; 0 c. From :1: : 0 to :1: : 3:1 and from :r: : $3 to m : :35 (overthe intervals [0, 3:1] and [$3, 315]). 0 cl. From :1: : $1 to m : 3:3 (over the interval [321, 33]}. At which of the marked mvalues is the value of the first derivative f'(;1:) decreasing? O a. 3:1, 3:2, and 335 O b. 31,34, and 335 O c. 3:2 and 323 Q d. 3:3 and 3:4 For the graph of the function 3' shown below, find the twosided limit 11111 f(:l'i). m>1 O a. 11111 f(:13) : 2 1311 0 in. 11111 f(:13) : 1 1311 0 c. 11111f(;1:) : 1 1311 0 1. 11111 f(:13) does not exist (DNE) 1311 \fThe graph shown below gives the position s of a particle as a function f(t) of time t. At which of the labeled points is the velocity the least (i.e., most negative)? E B CD A F Oa. E Ob. A O c. F O d. C\fThe distance traveled by a particle is given by s : it) : t3, where s is in feet and t is in seconds. Estimate the instantaneous velocity of the particle at t : 2 seconds. 0 a. 12 feet per second 0 b. 24 feet per second 0 c. 4 feet per second 0 d. 6 feet per second
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


