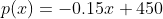
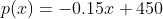
\fGiven that the cost function for manufacturing the chairs is C(x) =0.0002x -0.3x3 + 24x+95,000 where x is number of chairs and C(x) is price in dollars. 1. Find the marginal cost function, C'(x) 2. Find and interpret the marginal cost for x = 1000 units 3. Find the average cost function, C(x) 4. Find the marginal average cost function, C'(x) 5. Find and interpret the marginal average cost for x = 1000 units 6. Use the 1" derivative test to determine when the cost function is increasing and decreasing. Then, how many chairs (x) need to be produced in order to minimize the cost of production? What is the minimum cost? (Hint: use the quadratic formula AND round to 2 decimal places)