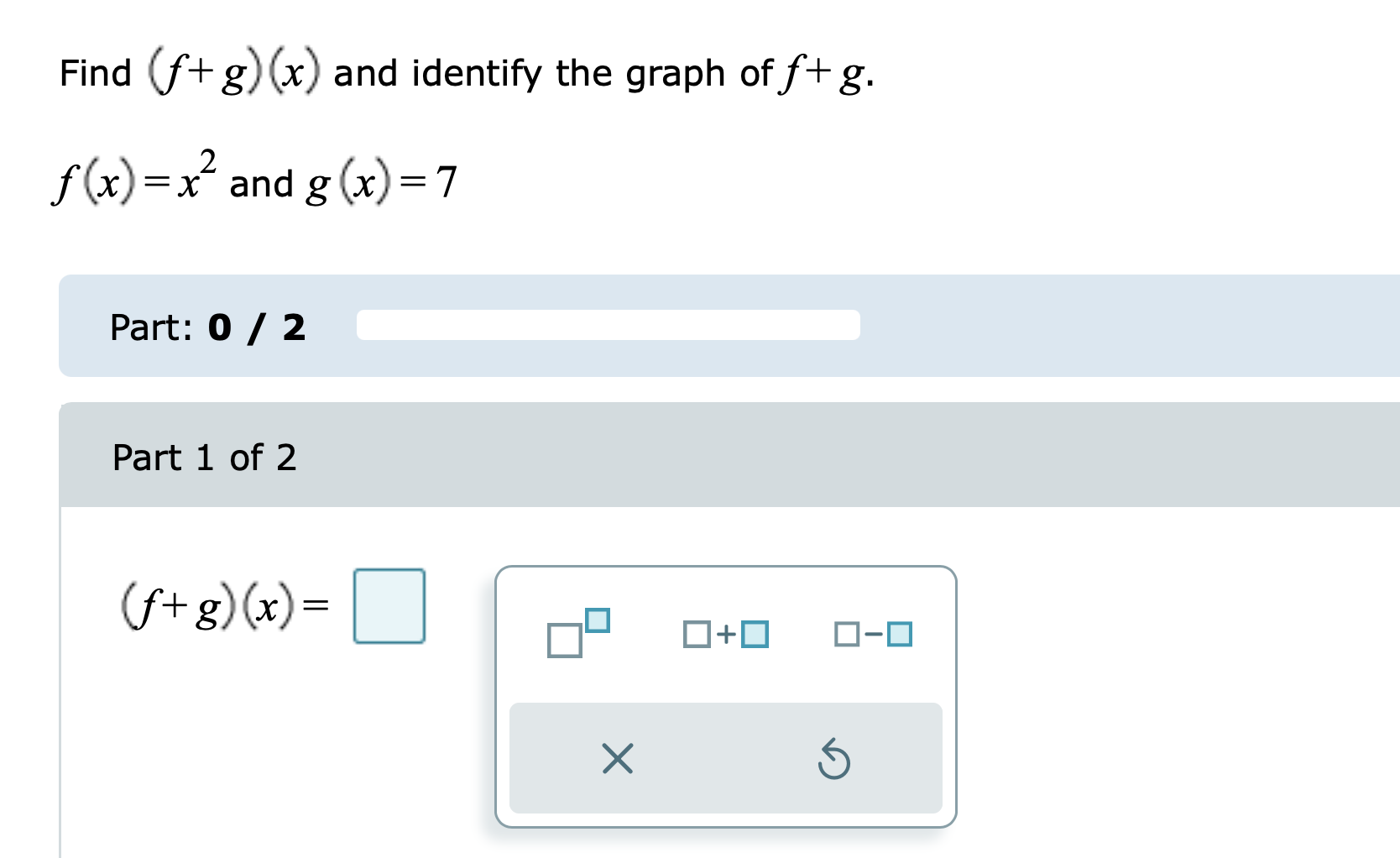
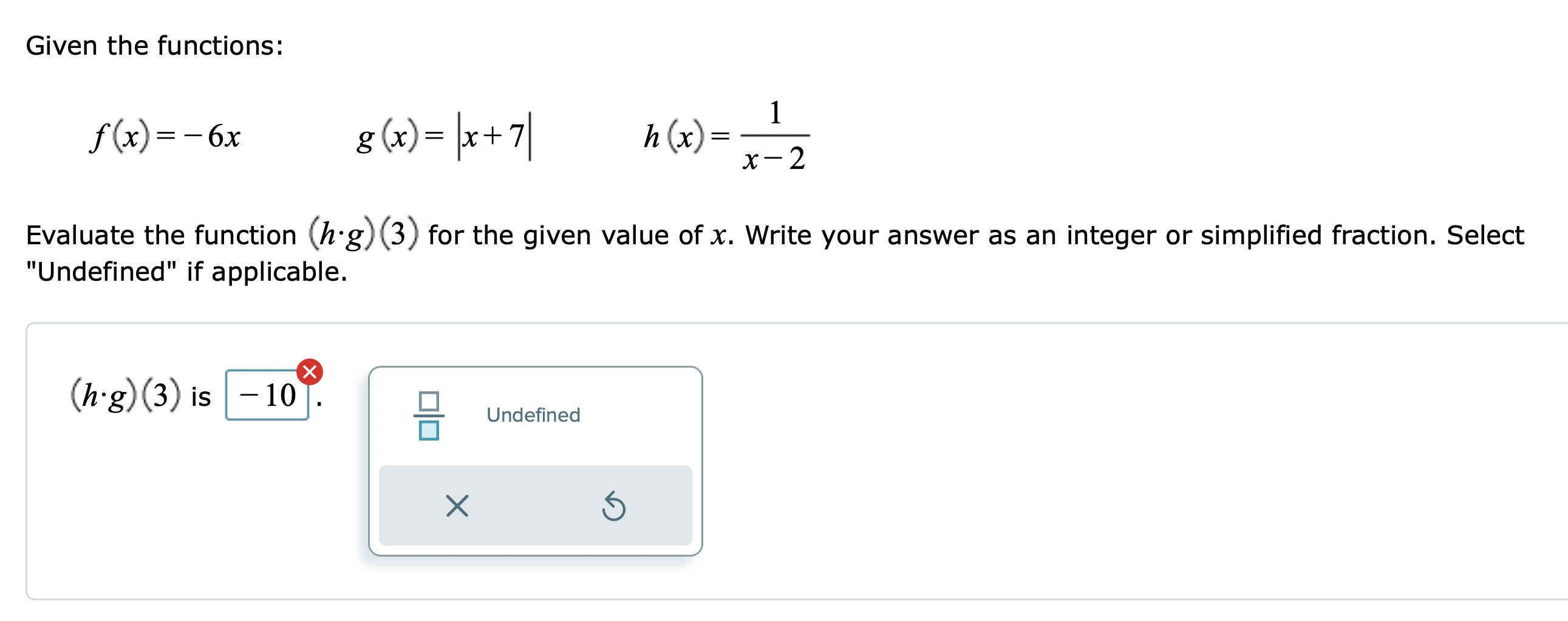
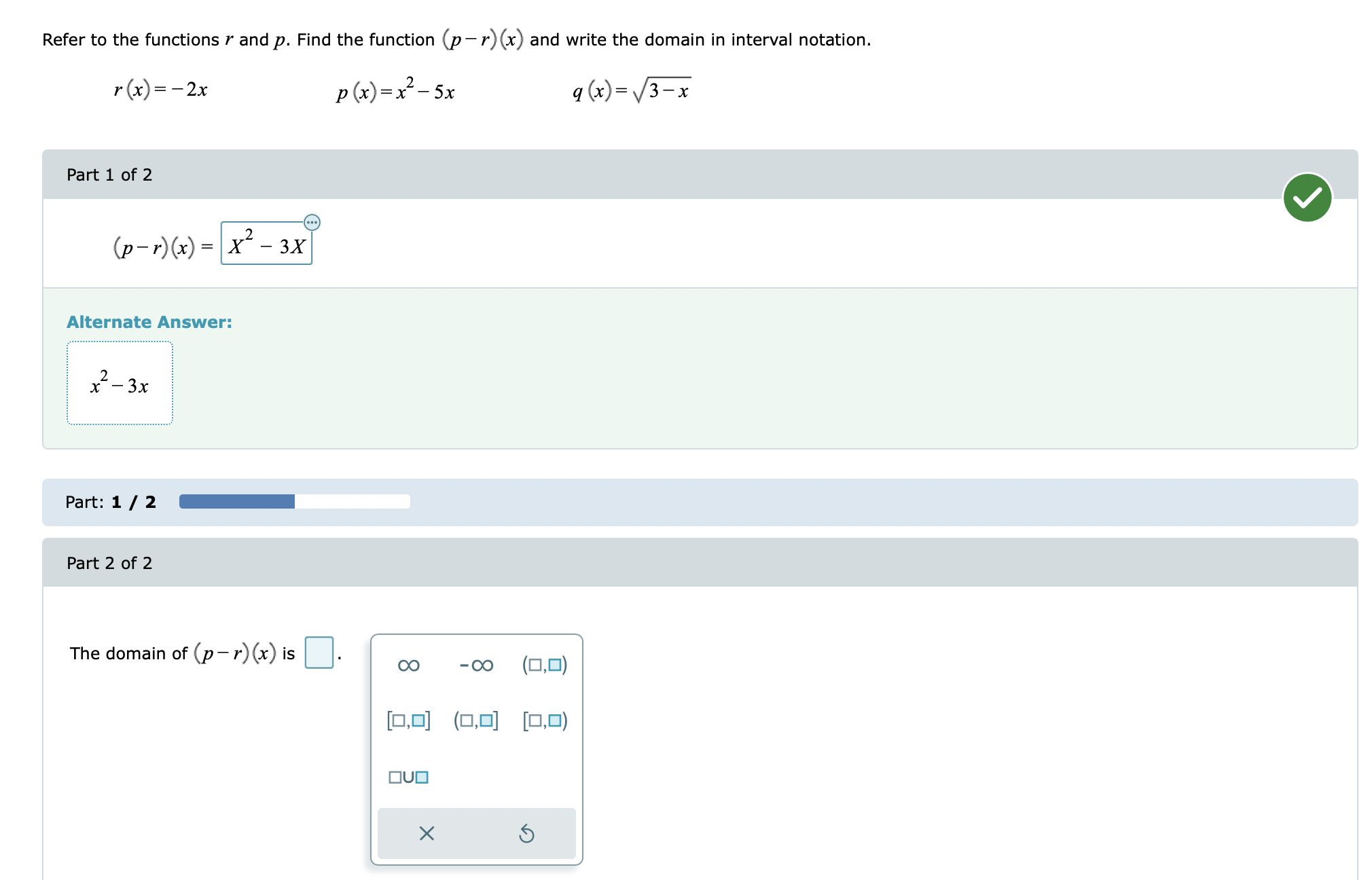
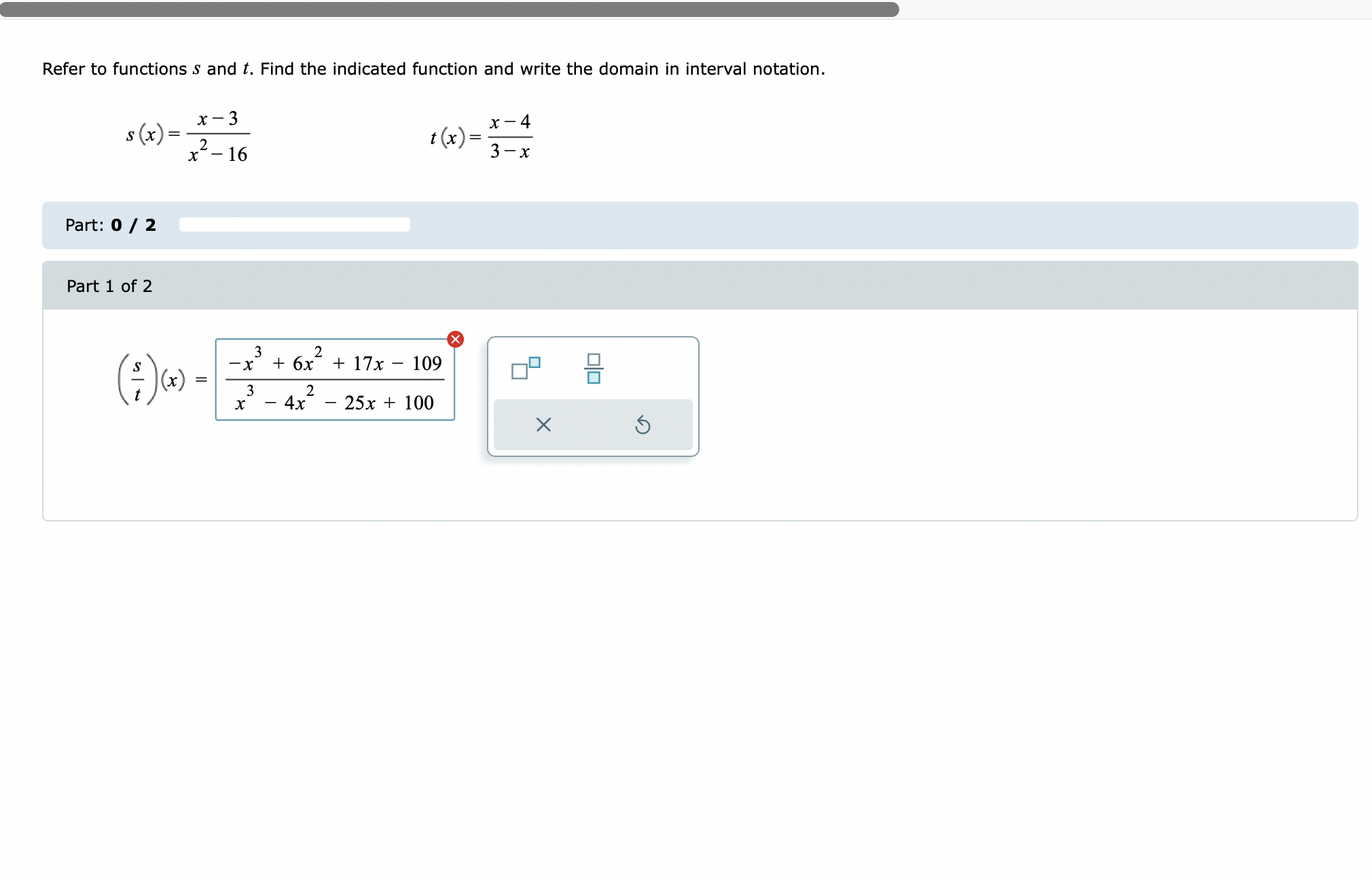
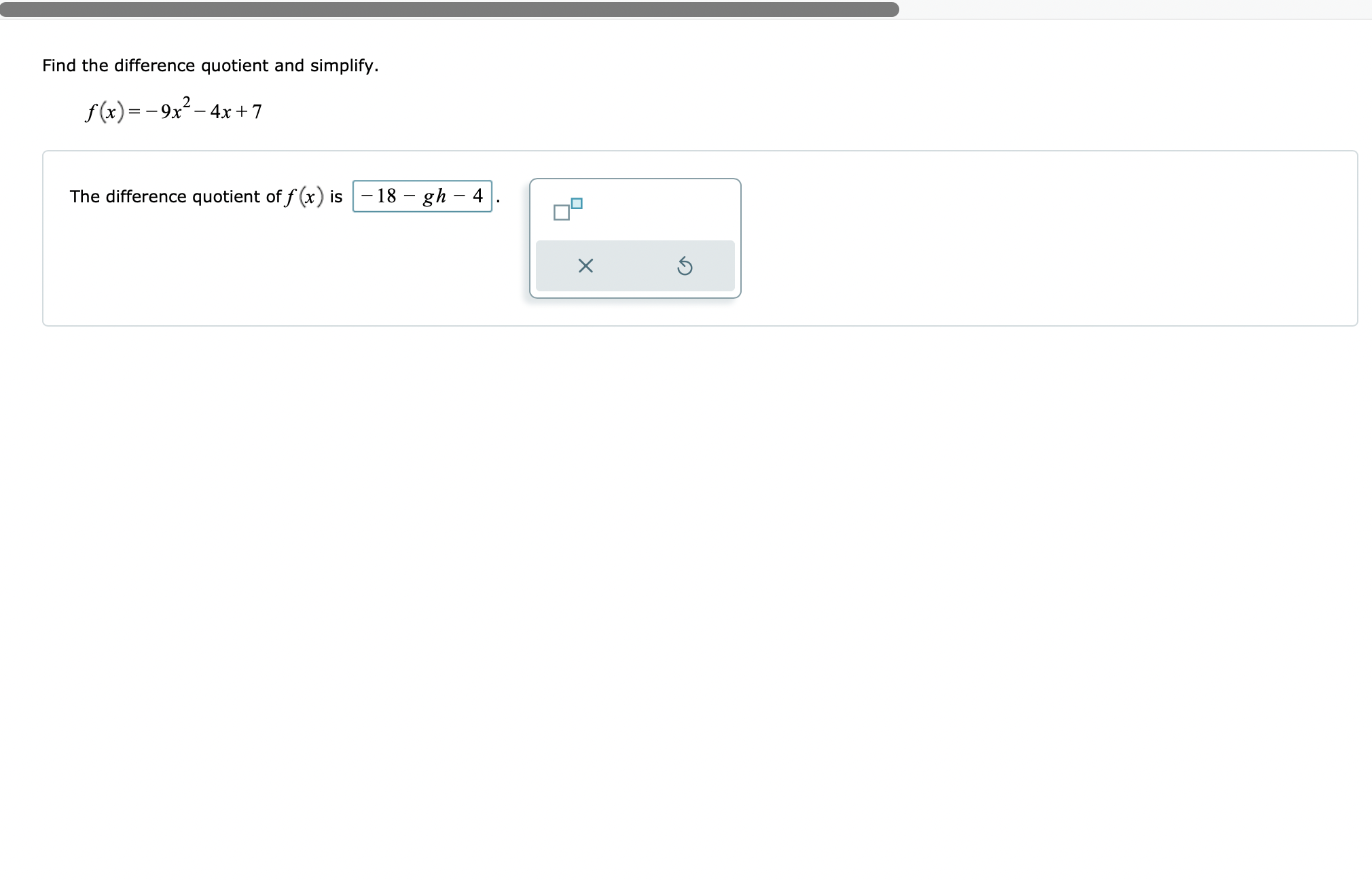
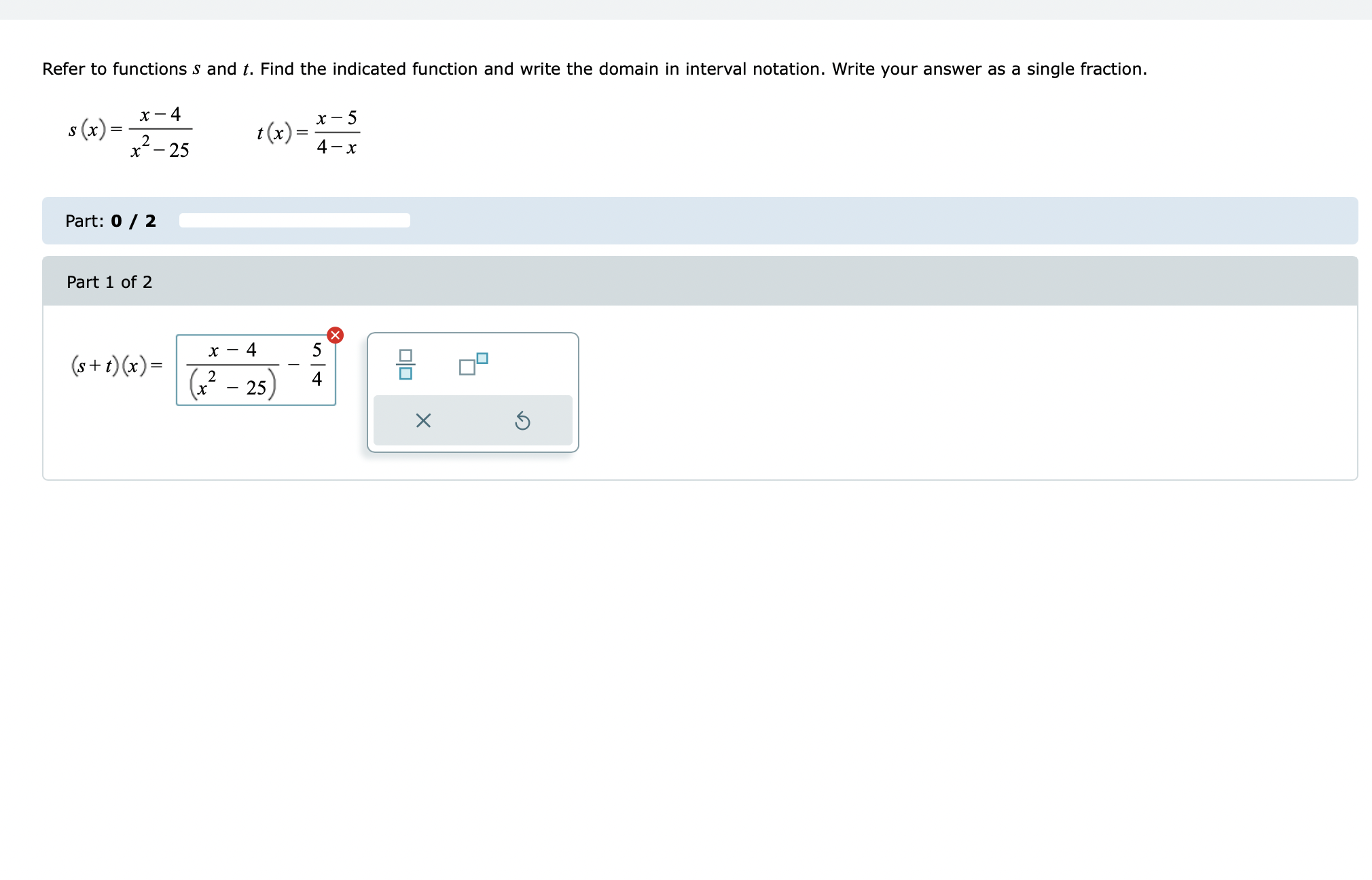
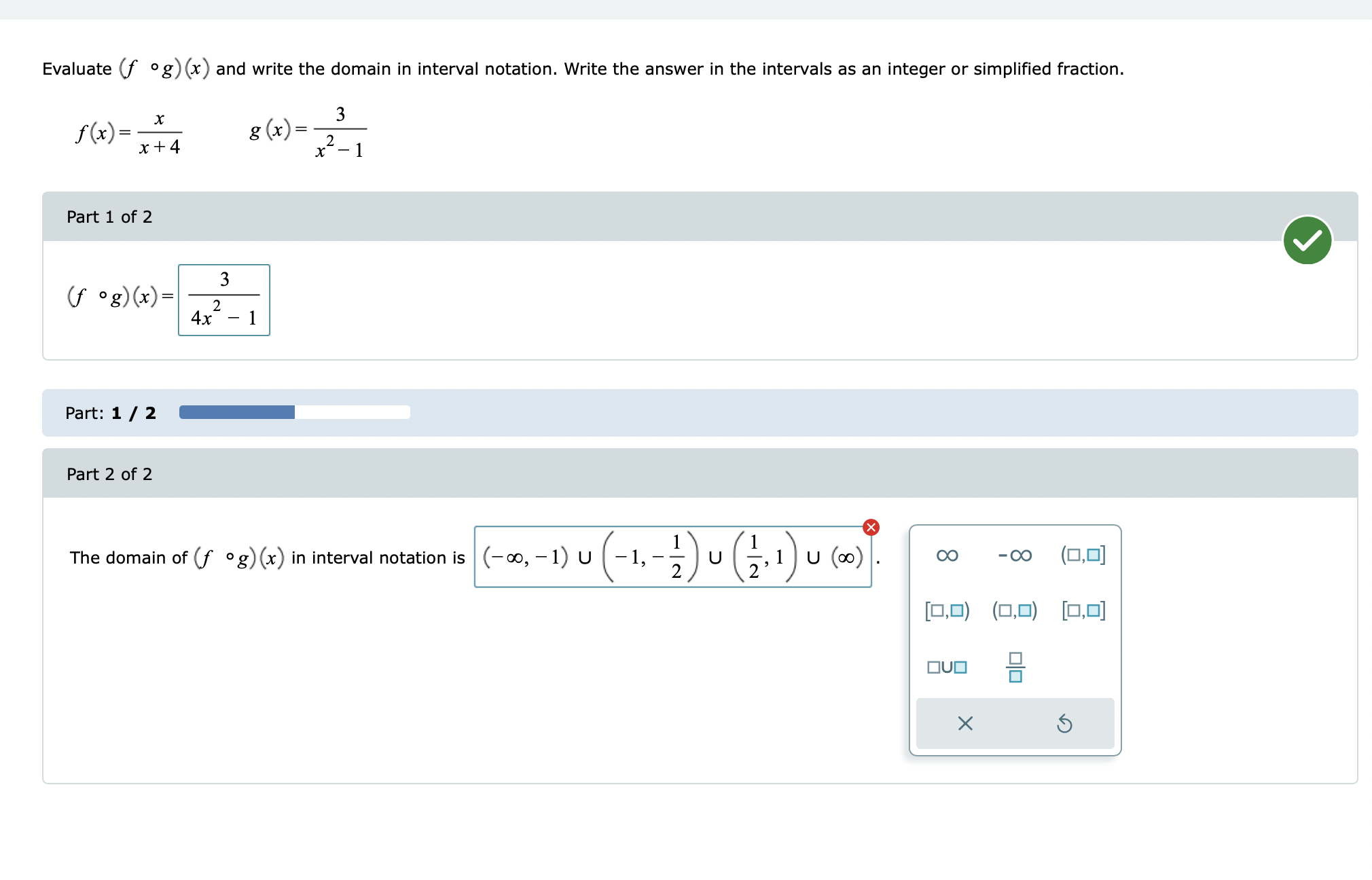
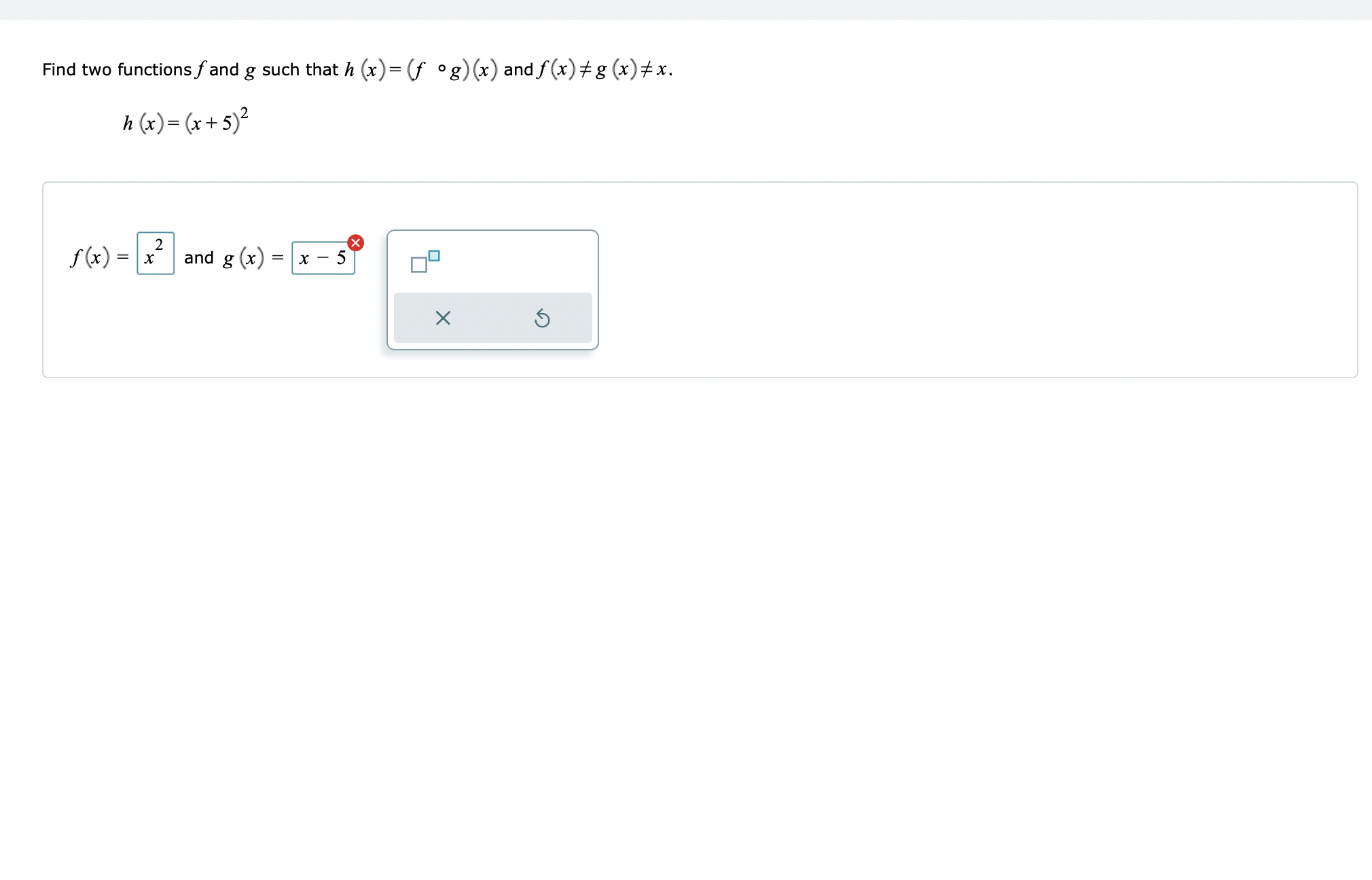
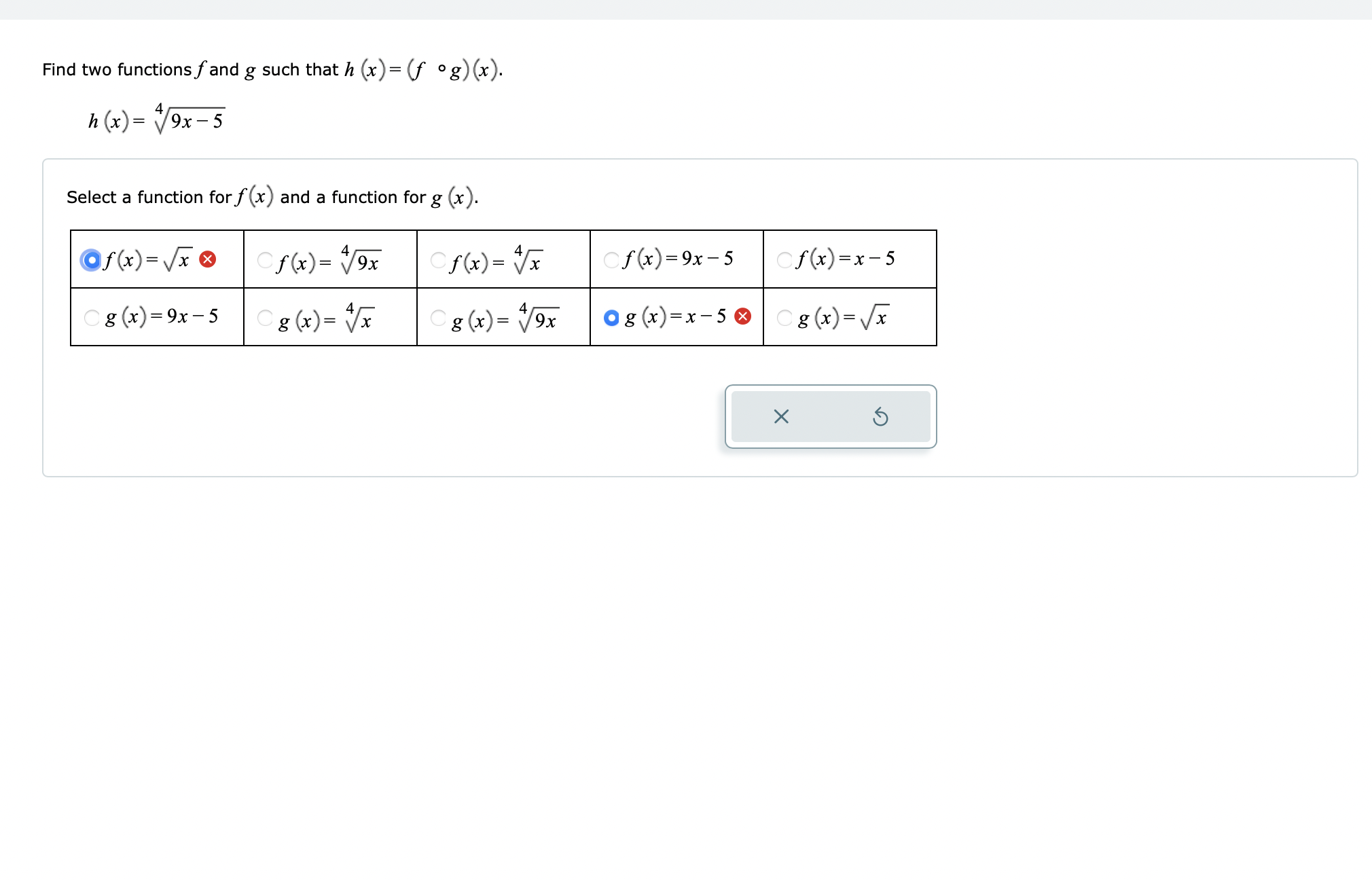
\fGiven the functions: f (x) = -6x g (x) = x+7 hx = x- 2 Evaluate the function (h.g) (3) for the given value of x. Write your answer as an integer or simplified fraction. Select "Undefined" if applicable. (h g) (3) is - 10 Undefined X 5Refer to the functions r and p. Find the function (p-r) (x) and write the domain in interval notation. r (x) =-2x p(x) =x- 5x 9 (x) = 3-x Part 1 of 2 V (p - r) (x) = x - 3X Alternate Answer: x - 3x Part: 1 / 2 Part 2 of 2 The domain of (p-r) (x) is. OO -00 (0,0) [0,0] (0,0] [0,0) OVO X 5Refer to functions 5 and t. Find the indicated function and write the domain in interval notation. s(x)= :_3 t(x)= \"4 x 16 3-1: -x3 + 6x2 + 17x 109 x3 4x2 25x + 100 Find the difference quotient and simplify. f(x)=9x24x+7 The difference quotient off(x) is 18 gh 4 . Refer to functions .9 and t. Find the indicated function and write the domain in interval notation. Write your answer as a single fraction. x-5 4x 4 2 t(x) = s(x)= xx Evaluate (f g) (x) and write the domain in interval notation. Write the answer in the intervals as an integer or simplified fraction. f( x ) = X 3 g x = x +4 x Part 1 of 2 V 3 (f g) (x) = 4x Part: 1 / 2 Part 2 of 2 The domain of (f g) (x) in interval notation is (-co, -1) U -1, -2 ) U (2, 1 ) U (00) OO -00 (0,0] [0,0) (0,0) [0,0] OVO X 5\fFind two functions f and g such that h (x) = (f . g) (x). h (x ) = $9x - 5 Select a function for f (x) and a function for g (x). of(x) =x Of ( x) = V9x Of ( x ) = Vx Of(x) =9x -5 Of (x ) = x-5 Cg (x) =9x - 5 Cg (x)= Vx Cg(x) = Vox Og( x) =x-50 Cg(x) = x X 5