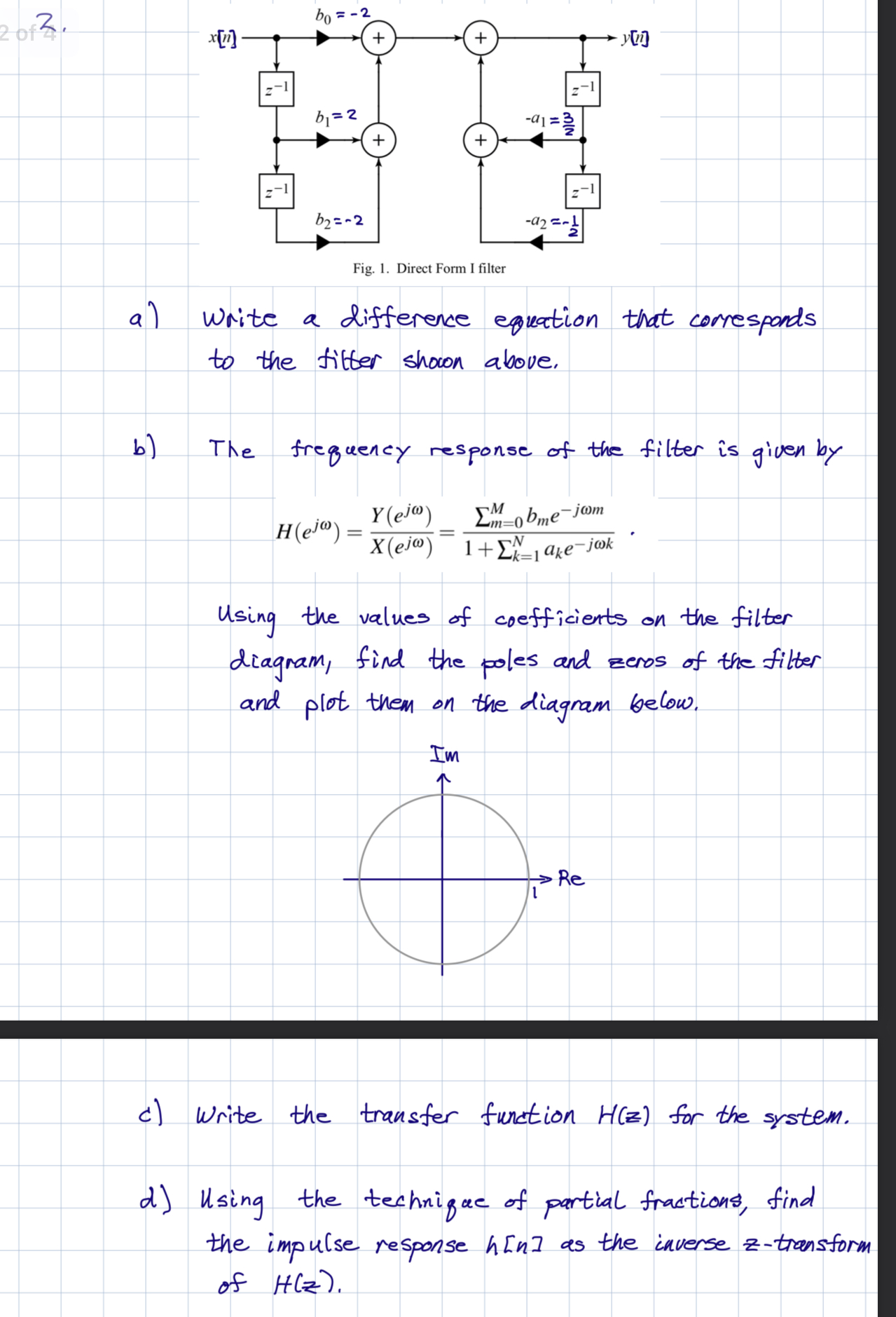
Fig. $1.$ Direct Form I filter

aH$($e$^($j$\backslash$omega $))=($Y$($e$^($j$\backslash$omega $)))/($x$($e$^($j$\backslash$omega $)))=(\backslash$sum$\_($m$=0)^$M b$\_($m$)$e$^(-$j$\backslash$omega m$))/(1+\backslash$sum$\_($k$=1)^$N a$\_($k$)$e$^(-$j$\backslash$omega k$)).$

Using the values of coefficients on the filter

diagram, find the poles and zeros of the filter

and plot them on the diagram below.

cH$($z$)$ for the system.

dh$[$n$]$ as the inverse z$-$trensform

of H$($z$).$ Fig. $1.$ Direct Form I filter

aH$($e$^($j$\backslash$omega $))=($Y$($e$^($j$\backslash$omega $)))/($x$($e$^($j$\backslash$omega $)))=(\backslash$sum$\_($m$=0)^$M b$\_($m$)$e$^(-$j$\backslash$omega m$))/(1+\backslash$sum$\_($k$=1)^$N a$\_($k$)$e$^(-$j$\backslash$omega k$)).$

Using the values of coefficients on the filter

diagram, find the poles and zeros of the filter

and plot them on the diagram below.

cH$($z$)$ for the system.

dh$[$n$]$ as the inverse z$-$trensform

of H$($z$).$ e$)$ State whether the filter is stable or unstable and why.

f$)$ If just one of the coefficients of the filter $($hie one of $\text{'}\backslash ($ a $\backslash )\text{'}$ or $\text{'}\backslash ($ b $\backslash )\text{'}$ values$)$ is changed to the negative of its stated value, can the filter be made unstable? If so$,$ state why. If not, state why not.