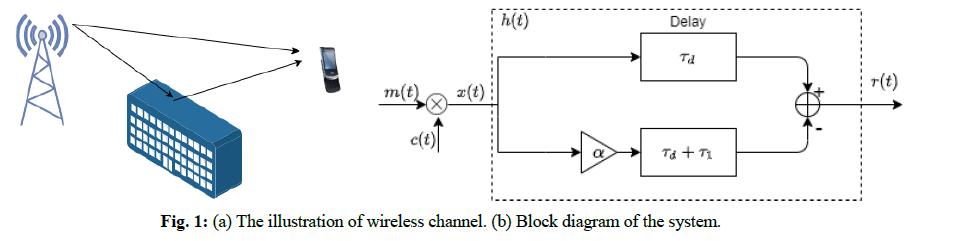
Fig. 1(a) illustrates a wireless communication system, where the message signal is denoted by m(t), the carrier signal is denoted by c(t). The transmitted radio signal is denoted by x(t) = m(t)c(t). In long distance radio links, the radio signal can be received by direct path between the transmitting and receiving antennas and also reflections by other objects, such as hills, buildings and so on. Assume the wireless communication channel is modeled with an LTI system, where the channel impulse response of this system is denoted by h(t), and the received signal r(t) = x(t) * h(t). a) Let M (f) denotes the Fourier transform of m(t). Find and express M(f) for m(t) = = 1 A/2t -(t-B) e 2A (A HTNB #TN: team number). (Hint-1: Consider time-shifting E property, Hint-2: e-k dk = ) -00 b) Plot |M(f) and 4M(f) using MATLAB. (x-axis of the plots should be in between (f =[-])). From the plots what is the approximate bandwidth of the message signal? c) Let c(t) = cos(21ft). Find and express X(f). Plot |X(f) using MATLAB (x-axis of the plots should be in between (f = [-1.5fu, 1.5fu])). From the plots what is the approximate bandwidth of the message signal? Show that whether x(t) is an energy type signal or a power type signal. Calculate its energy or power. (fu= 2000 x #TN Hz) d) Find and express h(t), and the frequency response of the system, H(f), and its magnitude response [H(f)] and phase response, 4H(f). (ta 100ta) = 0.1 , T = e) Plot H(f)], [R()], 4H(), 4R() using MATLAB. (x-axis of the plots should be in between f-[-1.5fu,1.5fu)). m(t) x(t) h(t) Delay Td Ta + Ti Fig. 1: (a) The illustration of wireless channel. (b) Block diagram of the system. r(t)