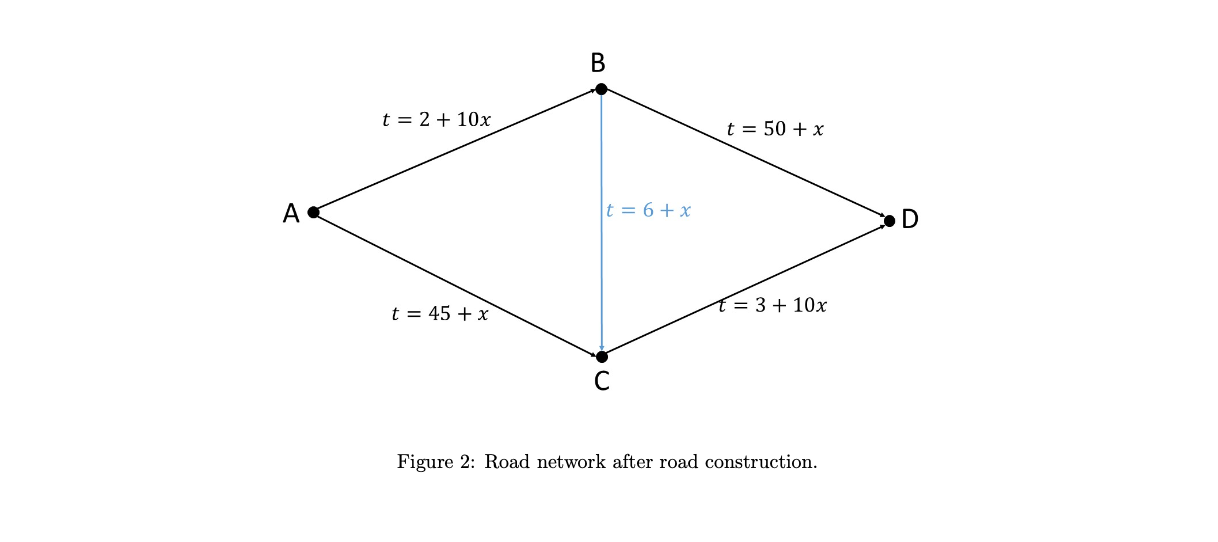
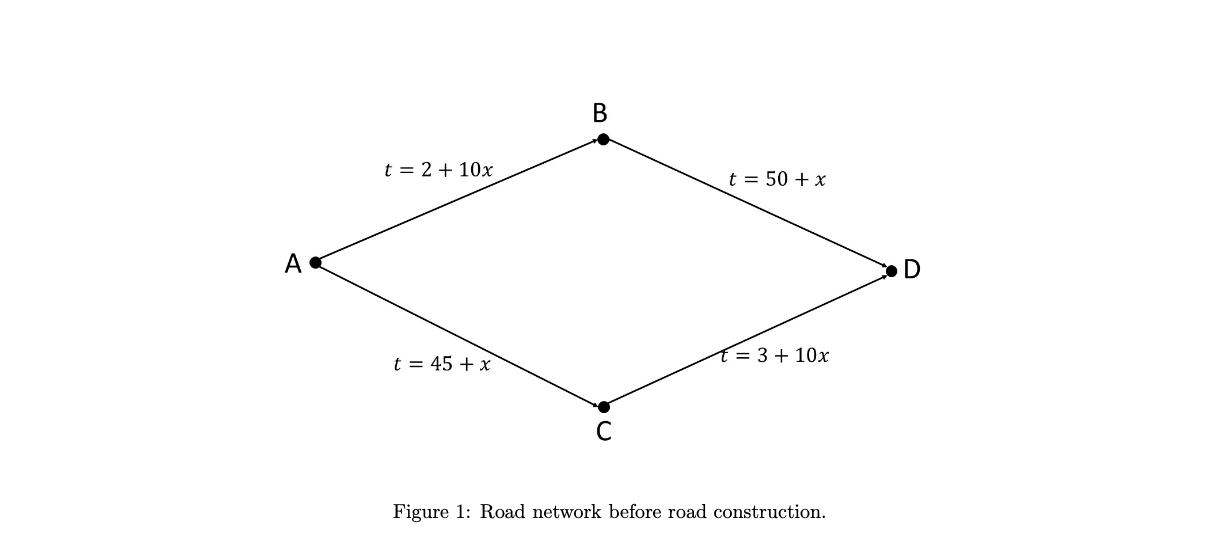
Figure 1 shows a road network. There are 4000 drivers (whom we consider to be infinitely divisible because we're economists) at point A who wish to get to point D. The equations along each of the branches indicate how long that branch takes to travel when x drivers choose to use it (they are nondecreasing functions due to congestion). Part (a). Common sense suggests that if you noticed that one route was faster than your route, you would instead choose to use the faster route. Use this fact to give in words an equilibrium condition for the road system. Subsequently express this mathematically, and use this to find the journey times along each of the routes. Part (b). This question attracts no marks but I'd like you to consider it and give an answer with justification regardless - if there is no evidence in your submission that you thought about this before proceeding, you will lose marks. In general, what effect do you expect the introduction of a new road would have on journey times and why? Part (c). A new road is added, as shown in figure 2. Repeat part (a) for the new road system. Are you surprised by the results? A t = 2 + 10x t = 45 + x B t = 6 +x t = 50 + x = 3 + 10x Figure 2: Road network after road construction. D A t = 2 + 10x t = 45 + x B t = 50 + x = 3 + 10x Figure 1: Road network before road construction.