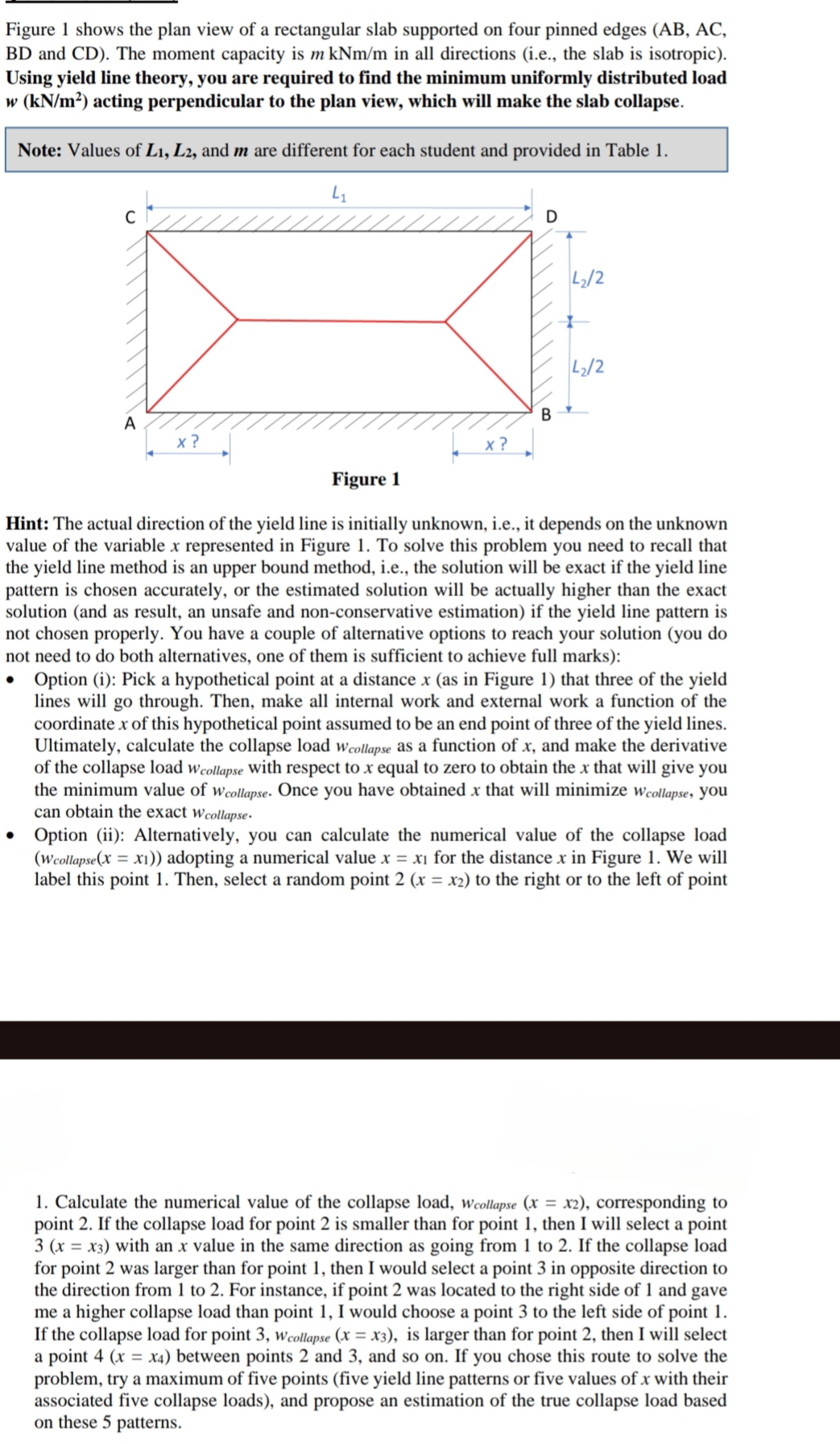
Figure $1$ shows the plan view of a rectangular slab supported on four pinned edges $,$ BD and CD $).$ The moment capacity is $mkN\frac{m}{m}$ in all directions $($i$.$e$.,$ the slab is isotropic$).$ Using yield line theory, you are required to find the minimum uniformly distributed load $w(k\frac{N}{m^2})$ acting perpendicular to the plan view, which will make the slab collapse.

Note: Values of $L_1,L_2,$ and $m$ are different for each student and provided in Table $1.$

Hint: The actual direction of the yield line is initially unknown, i$.$e$.,$ it depends on the unknown value of the variable $x$ represented in Figure $1.$ To solve this problem you need to recall that the yield line method is an upper bound method, i$.$e$.,$ the solution will be exact if the yield line pattern is chosen accurately, or the estimated solution will be actually higher than the exact solution $($and as result, an unsafe and non$-$conservative estimation$)$ if the yield line pattern is not chosen properly. You have a couple of alternative options to reach your solution $($you do not need to do both alternatives, one of them is sufficient to achieve full marks$)$:

Option $($i$)$: Pick a hypothetical point at a distance $x($as in Figure $1)$ that three of the yield lines will go through. Then, make all internal work and external work a function of the coordinate $x$ of this hypothetical point assumed to be an end point of three of the yield lines. Ultimately, calculate the collapse load $w_{\text{c}\text{o}\text{l}\text{l}\text{a}\text{p}\text{s}\text{e}}$ as a function of $x,$ and make the derivative of the collapse load $w_{\text{c}\text{o}\text{l}\text{l}\text{a}\text{p}\text{s}\text{e}}$ with respect to $x$ equal to zero to obtain the $x$ that will give you the minimum value of $w_{\text{c}\text{o}\text{l}\text{l}\text{a}\text{p}\text{s}\text{e}}.$ Once you have obtained $x$ that will minimize $w_{\text{c}\text{o}\text{l}\text{l}\text{a}\text{p}\text{s}\text{e}},$ you can obtain the exact $w_{\text{c}\text{o}\text{l}\text{l}\text{a}\text{p}\text{s}\text{e}}.$

Option $($ii$)$: Alternatively, you can calculate the numerical value of the collapse load $($