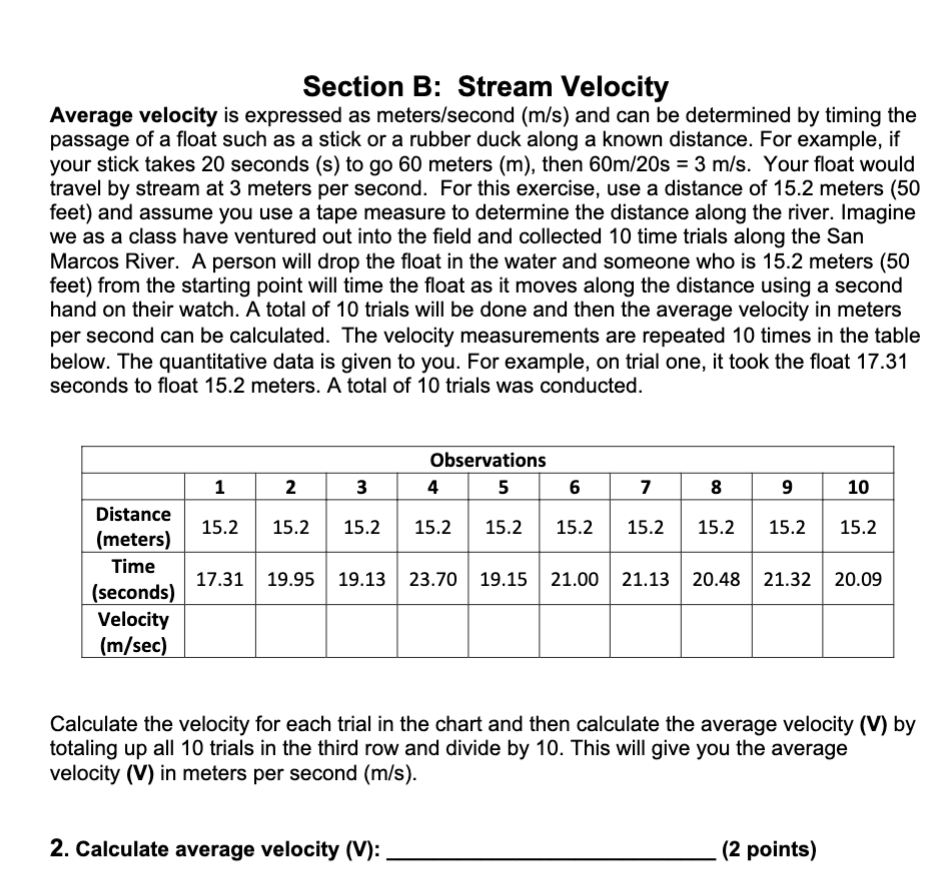
Figure 2: San Marcos River Using your data from the San Marcos River (Figure 2) determine the cross-sectional area (A of the stream. Imagine that you went out to the river and measured the width and depth of stream. This data is given to you below. Steps: - Measure the width of the stream. Width = 18.2 meters . Measure the depth of the stream. Depth = 2.8 meters 1. Calculate the cross-sectional area. (width X depth will be in square meters (m2) Cress-sectional area (A) = (1 point} Section B: Stream Velocity Average velocity is expressed as meters/second (m/s) and can be determined by timing the passage of a float such as a stick or a rubber duck along a known distance. For example, if your stick takes 20 seconds (s) to go 60 meters (m), then 60m/20s = 3 m/s. Your float would travel by stream at 3 meters per second. For this exercise, use a distance of 15.2 meters (50 feet) and assume you use a tape measure to determine the distance along the river. Imagine we as a class have ventured out into the field and collected 10 time trials along the San Marcos River. A person will drop the float in the water and someone who is 15.2 meters (50 feet) from the starting point will time the float as it moves along the distance using a second hand on their watch. A total of 10 trials will be done and then the average velocity in meters per second can be calculated. The velocity measurements are repeated 10 times in the table below. The quantitative data is given to you. For example, on trial one, it took the float 17.31 seconds to float 15.2 meters. A total of 10 trials was conducted. Observations 1 2 3 4 5 6 7 8 9 10 Distance 15.2 15.2 15.2 15.2 15.2 15.2 15.2 15.2 15.2 (meters) 15.2 Time 17.31 19.95 19.13 23.70 19.15 21.00 21.13 20.48 21.32 20.09 (seconds) Velocity (m/sec) Calculate the velocity for each trial in the chart and then calculate the average velocity (V) by totaling up all 10 trials in the third row and divide by 10. This will give you the average velocity (V) in meters per second (m/s). 2. Calculate average velocity (V): (2 points)Discharge (0) To calculate discharge (0). multiply the cross-sectional area (A) x average velocity (V). O = AV This will be in cubic meters per second. (m3isec) 3. Q = (1 point) Daily Flow What is the daily volume of water that ows through this river? Your answer should be in 3 cubic meters per day (m iday). To do this multiply the discharge times 60 X 60 X 24. 60 (50 seconds i 1minute) X 60 {50 minutes! 1 hour} X 24 (24 hours! 1 day) 4. Daily flow: (1 point) Section C: Wetted Perimeter You will need to measure the portion of water in the stream that comes in contact with the channel bank. This must be in meters (m). The wetted perimeter can be calculated as width plus 2 times the depth (w + 2d). It is the length of the channel cross-section that is wet. For this lab we will approximate the wetted perimeter by using the channel width plus two times the average depth (w + 2d). The wetted perimeter is calculated for you. Width (w) Wetted Perimeter = 23.8 m3 4 [LA/L} Depth (d) I 1 Depth (d) Section F: Mannings Equation You calculated velocity earlier in the exercise using only the surface of the river. For the remainder of this exercise. you will use Mannings equation to calculate velocity. Mannings Equation calculates the average velocity and is a more accurate way to determine stream velocity. Mannings equation calculates the average velocity of a stream taking into account all the characteristics of a stream such as the slope of a channel. the depth of the water. the roughness of the channel, and the shape of the channel. By using the Mannings equation. velocity is controlled by the following channel characteristics: hydraulic radius, channel slope, and roughness of channel. Hydraulic radius (R) the measw'e of the proportion of water in a stream that comes in contact with the channel bed or banks. Refer to section A for cross- sectional area and section C for wetted perimeter formulas. Show your work in the space below. R = cross-sectional area I wetted perimeter 5. R = (2 points) Channel slope (S) s = .02 Roughness of channel (n) n = .035 Mannings Equation V=E*R.s'rts.5 It You will need to use a scientic calculator to calculate the equation. Tor the hydraulic radius (R) and slope {5), you will need to use the Y" key on the calculator. For example, 7.1357 = 3.72. On your calculator, punch in 7.13, and then hit the Y" and punch in .67. V: misec R = hydraulic radius (cross-sectional area of the channel divided by the wetted perimeter) S = slope or gradient of the channel n = roughness coefcient Enter the San Marcos river stream data in the table below from the previous sections. Width (w) Average Depth (d) Cross-sectional area (A) Wetted Perimeter (w + 2d) Hydraulic radius (R Stream gradient (S) Roughness Coefficient (n) 6. Using Mannings equation: a) What was the velocity? Show your work. (3 points) b) Using your answer from 6a, what was the discharge? Q =AV Show your work. (2 points) c). Using your answer from 6b, calculate the daily volume of water that flows through this river. Show your work. (1 point) 7. What are the effects of floods on the stream compared to average flows on erosion and moving sediment? (1 point) 8. If this same stream should enter a broader channel with the same discharge (Q), what would happen to the velocity? (1 point)