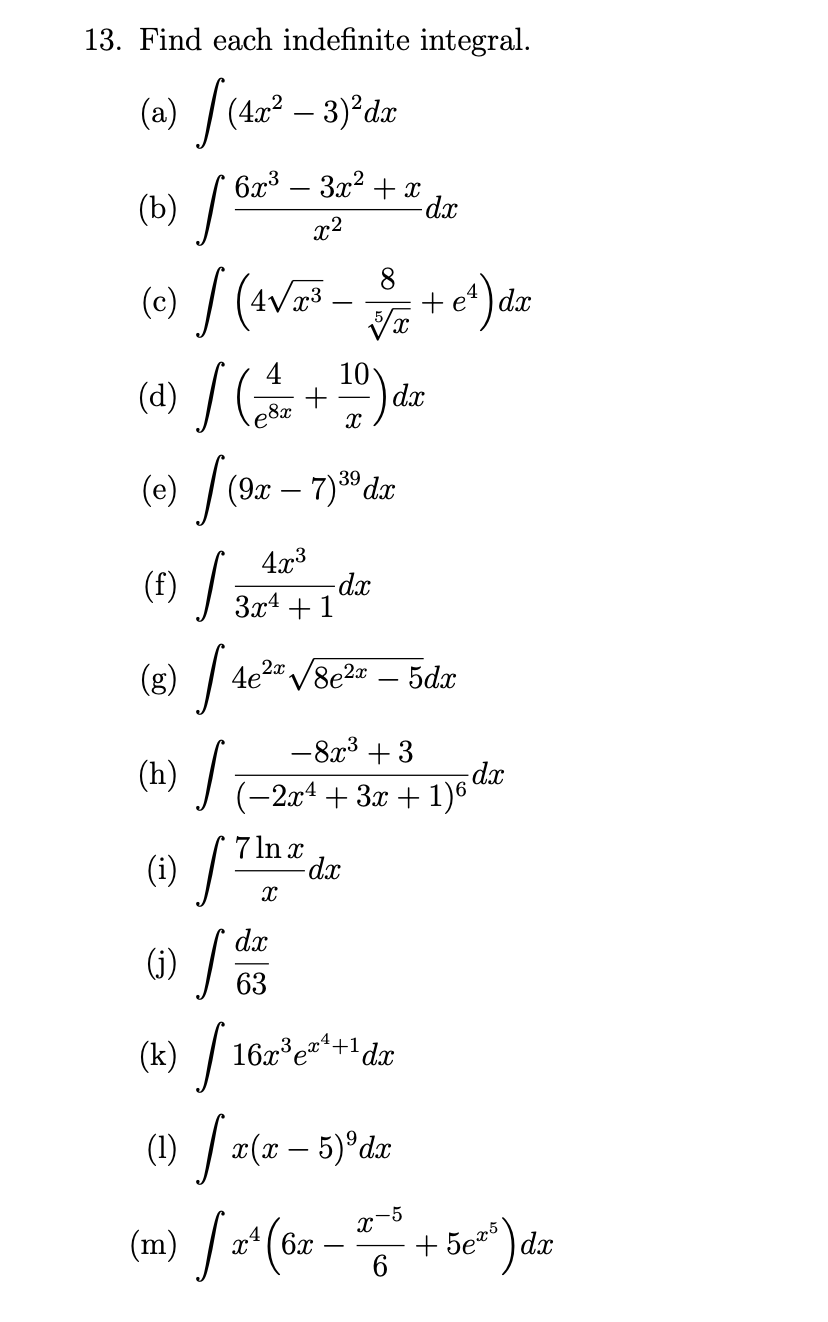
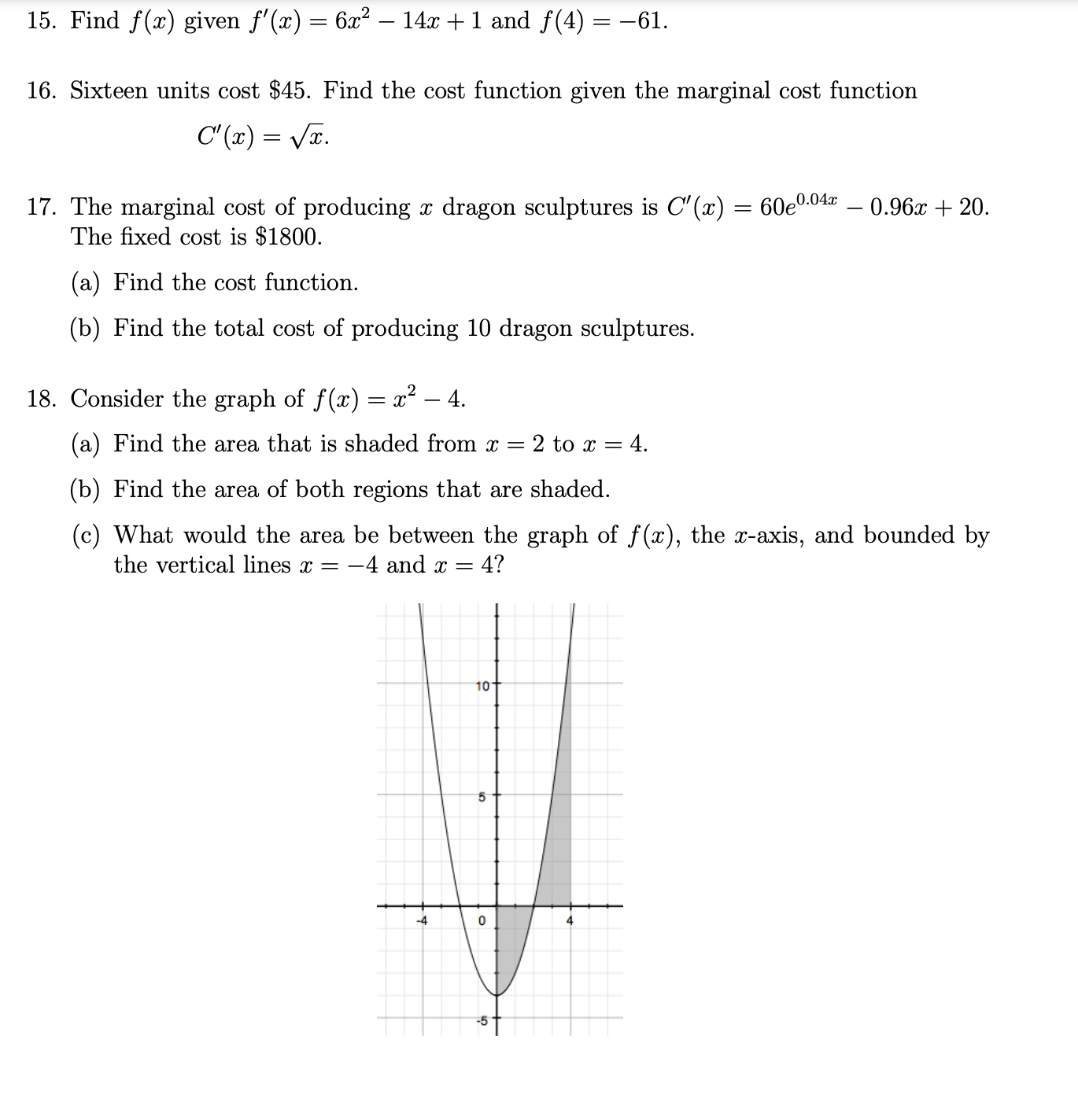
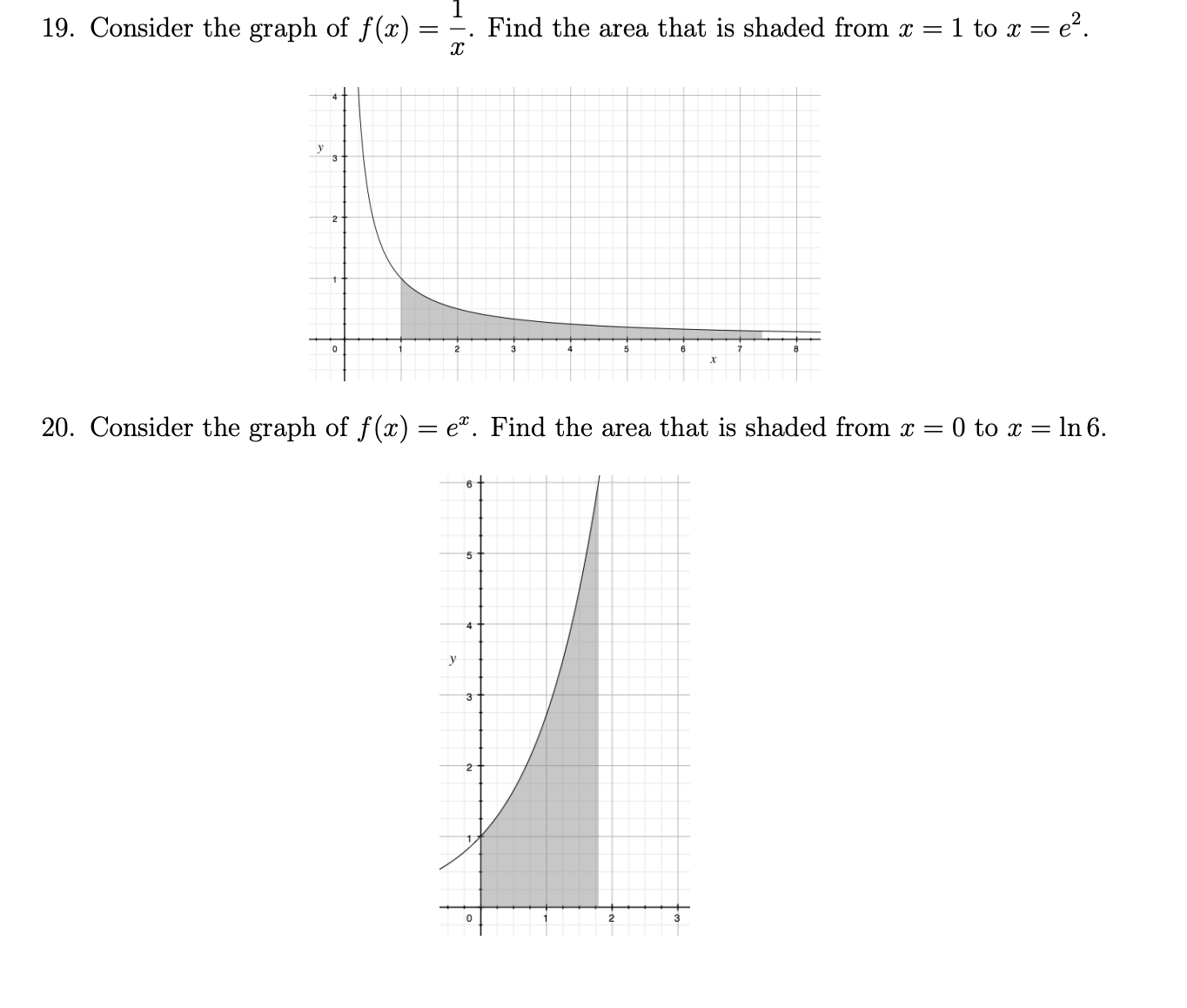
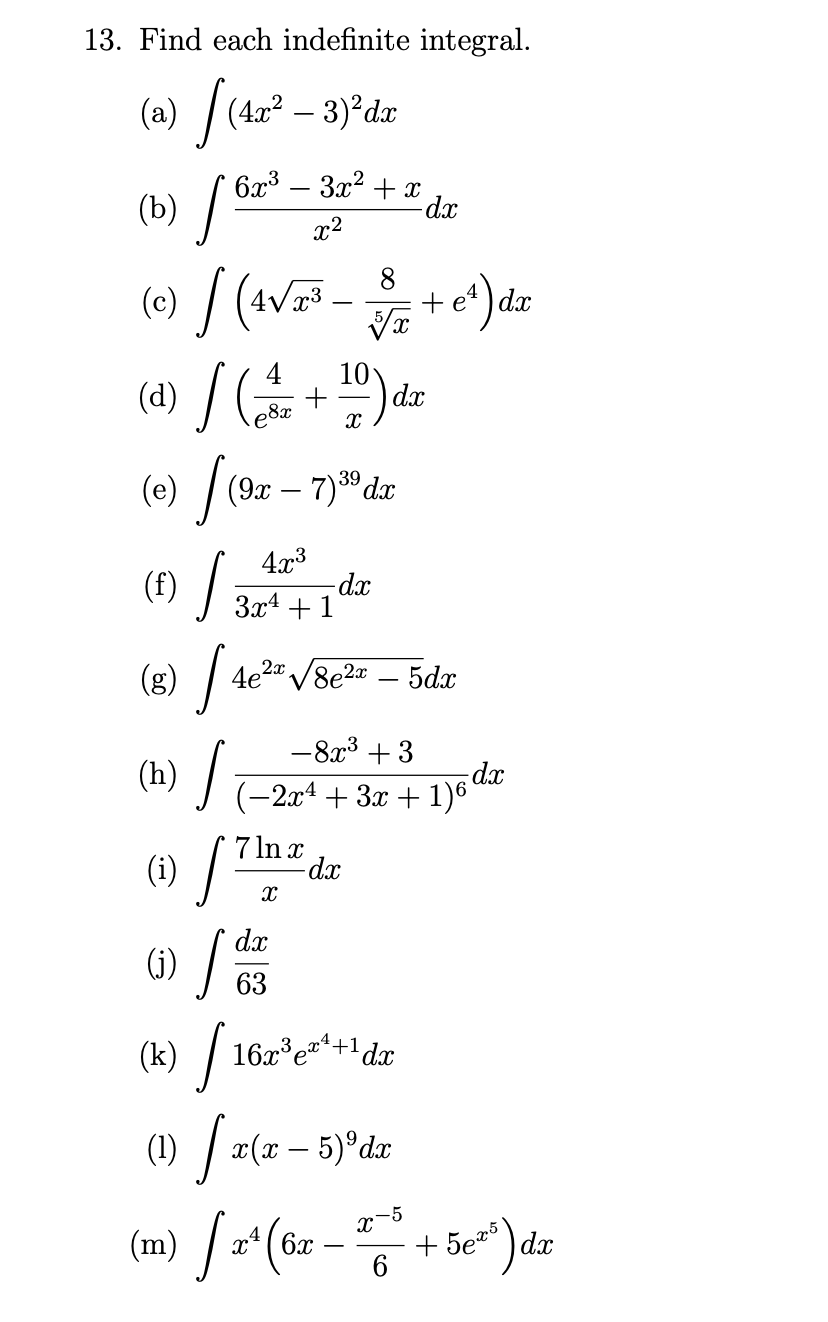
Final Exam Review Practice Problems 1. Let 9(56) = (3:2 1)3. Find g). 2. The height 3 of a ball thrown straight up with an initial speed of 80 feet per se (ft / sec) from a rooftop 96 feet high is s = 3(t) = 16t2 + 8013 + 96 where t is the elapsed time that the ball is in the air. The ball misses the rooftc its way down and eventually strikes the ground. (a) Find the height of the ball at t = 2 seconds. (b) Find the instantaneous velocity of the ball at t = 2 seconds. (c) Find the acceleration of the ball at t = 2 seconds. 3. Use the second derivative test to nd the relative extrema of f (x) = m3 12x. 4. For each function below, determine the intervals on which f (as) is concave upwarc concave downward and identify the siccoordinates of any inection points. (a) f (at) = :c4 23c3 + 72x2 13 (h) f (at) = 23:4 + 6x3 125::2 + 8 1 1 (c) at) = $376 x'r' 3:4 +3x+ 20 5. Given the simplied forms of the rst and second derivatives of f (3:) = 2a: In (33: determine the intervals where f (x) is concave upward and downward and identi sircoordinates of any inection points. , _6x1 ,, _ 9 f($)_3x+1 f(x)_(3$+1)2 6. Find the absolute extrema of each function on the given interval. (a) f (x) = (3:2 - U2 [-2, 2] (b) f(x) = :c3 + 63:2 + 1 [1,6] 6. Find the absolute extrema of each function on the given interval. (a) f0?) = ($2 U2 [2, 2] (b) at) = :c3 + 63:2 + 1 [1,6] (c) f(.'13)= x2 8lnm [1,4] ((1) f0?) = 37 + 97333 [12 3] (e) re) = 3:64 263:3 + 603::2 11 [2, 1] 7. A production facility is capable of producing 60, 000 widgets in a day and the total daily cost of producing an widgets is given by 0(3). 200, 000, 000 C(56) = 250, 000 + 0.083: + f, 0