Question: Find 13 3 dA over the region R = {(x, y) | 0 x 4, 0 y 3} by identifying it as the volume

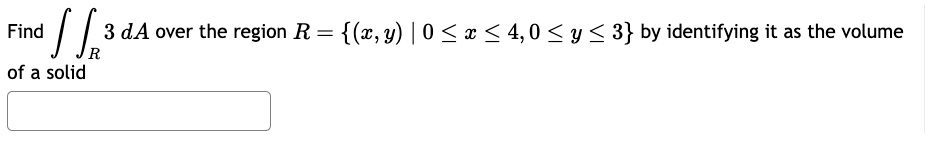
Find 13 3 dA over the region R = {(x, y) | 0 x 4, 0 y 3} by identifying it as the volume of a solid Suppose that f(x, y) = 4x + 5y and the region D is given by {(x, y) | 1 x 5, 1 y 5}. D a Then the double integral of f(x, y) over D is f(x, y) dady = D Suppose that f(x, y) D = - and the region D is given by {(x, y) | 3 x 4, 3 y 6}. Then the double integral of f(x, y) over D is f(x, y) ddy Round your answer to four decimal places.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Funfair Limited a retailer specialised in selling kid toys. The company was established in 2002 in Bristol and has now been among the top three largest toy retailers in the South-West of England. It...

Suppose that the treasurer of IBM has an extra cash reserve of $100,000,000 to invest for six months. The interest rate is 11 percent per annum in the United States and 10 percent per annum in...

In Problem find the volume of the solid under the graph of f (x, y) over the region R bounded by the graphs of the indicated equations. Sketch the region R; the solid does not have to be sketched....

Score: 0/9 0/9 answered Question 1 Find 5 d.A over the region R = {(x, y) | 0 g(x, y) for all (x, y) in R. O True O False Question Help: Message instructor D Post to forum Submit Question MacBook Pro...

In Problems 1-3, find the volume of the given solid. First, sketch the solid; then estimate its volume; finally, determine its exact volume. 1. Solid under the plane z = x + y + 1 over R = {(x, y): 0...

MATH-1326-THQ 9, 2016-11-02 16:54 (Printed First Name) (Printed Last Name) \u0012 \u0013 XXX0000 Net ID (First Letter of Last Name) \u0012 \u0013 001 - 503 Section Take Home Quiz 9 Penalty...

Question 69 please 4-x2 xp 2y 68. dy dx 4 69-74. Regions between surfaces Find the volume of the following solid regions. 69. The solid above the region R = { (x, y) : 0 = x=1, 0sys1-x} bounded by...

Find the volume of the following solid regions. The solid above the region R = {(x, y): 0 x 1, 0 y 2-x} and between the planes - 4x - 4y + z = 0 and-2x = y + z = 8 xY -2x -y +z = 8 R -4x - 4y + z...

Find the volume of the following solid regions. The solid above the region R = {(x, y): 0 x 1, 0 y 1-x} bounded by the parabo- x + y and loids z = z = 2x - y and the coordinate planes in the...

Graham purchased a business by agreeing to make three payments of $12 000 each in one year, two years, and four years. Because of cash flow difficulties in the first year, he renegotiated the payment...

Suppose your elasticity of demand for your parking lot spaces is 0.5, and price is $20 per day. If your MC is zero, and your capacity at 9 A.M. is 96%full over the last month, are you optimizing?

Hatfield Industries is a large manufacturing conglomerate based in the United States with annual sales in excess of $300 million. Hatfield is currently under investigation by the Securities and...

You are the CFO of a drug company, and you must decide whether to invest 70M dollars in R&D for a new drug. If you conduct the R&D, you believe that there is a 10% chance that the research...

Q 1 1) (P.A) (B.C) 2) P A /P(B.C) Q 2 1) (K f) (G.H) 2) (G.H) I 3) k / I

On October 1 of the current year a corporation sold, at par plus accrued interest, $1,000,000 of its 12% bonds, which were dated July 1 of this year. What amount of bond interest expense should the...

The income statement for Sweet Dreams Company is divided by its two product lines, blankets and pillows, as follows: If Sweet Dreams can eliminate total fixed costs of $30,000 by dropping the pillows...

The income statement for Sweet Dreams Company is divided by its two product lines, blankets and pillows, as follows: Sweet Dreams is considering eliminating the pillows product line. If they do so,...

Determine if the overhead allocated to the product relates to a single plantwide overhead rate method, multiple production department factory overhead rate method, or activity-based costing...

4.66 The paper cited in Exercise 4.65 also reported values of single-leg power for a low workload. The sample mean for n 5 13 observations was x 5 119.8 (actually 119.7692), and the 14th observation,...

4.67 The amount of aluminum contamination (in parts per million) in plastic was determined for a sample of 26 plastic specimens, resulting in the following data (The Log Normal Distribution for...

4.65 The paper The Pedaling Technique of Elite Endurance Cyclists (International Journal of Sport Biomechanics [1991]: 2953) reported the following data on single-leg power at a high workload: 244...