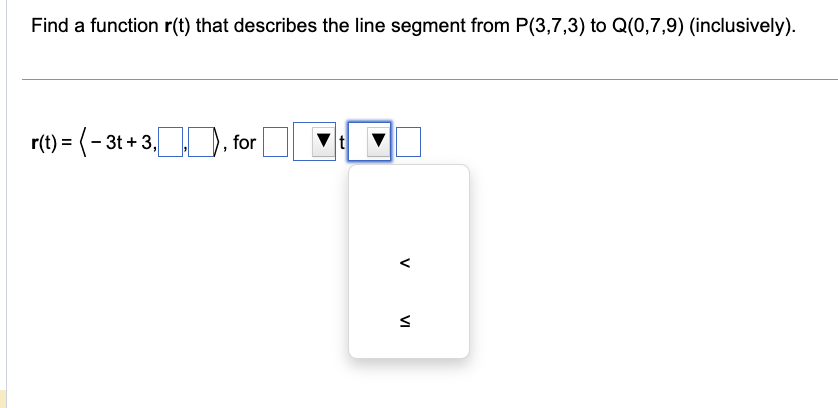
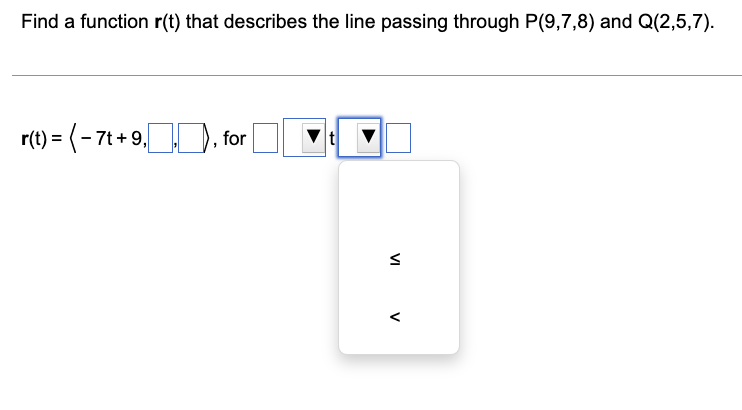
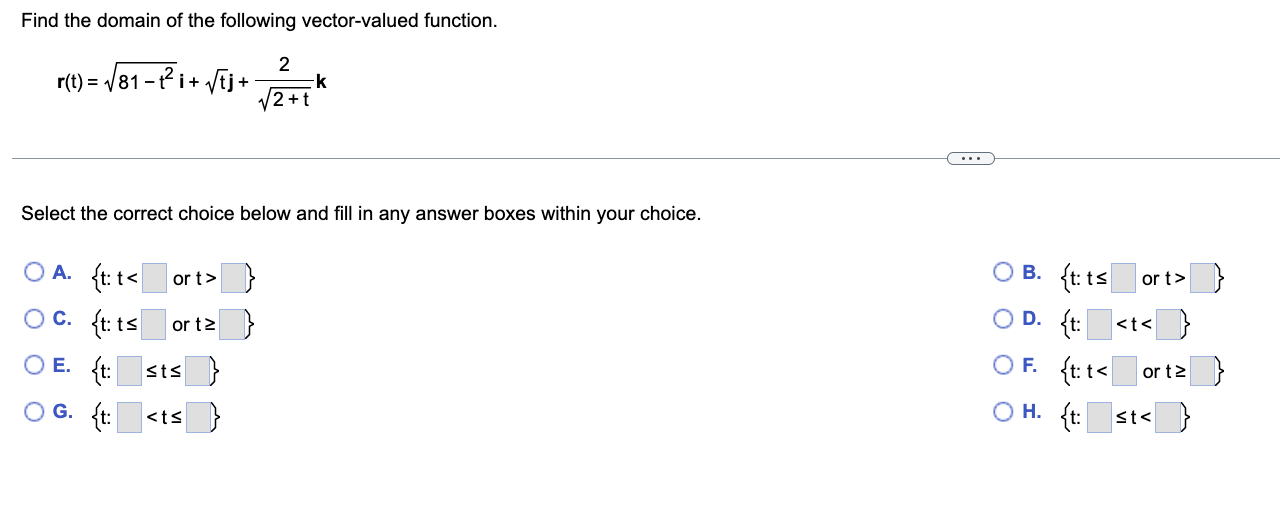
Find a function r(t) that describes the line passing through P(9,7,8) and Q(2,5,7). r(t) = (- 7t + 9, for t Find a function r(t) that describes the line segment from P(3,7,3) to Q(0,7,9) (inclusively). r(t) = (-3t+3,), for t V VI Find a function r(t) that describes the line passing through P(9,7,8) and Q(2,5,7). r(t) = (-7t + 9,, for t VI V Evaluate the following limit. lim t-0 lim t0 3 sin 2t 2t 3 sin 2t 2t 6t e et - 6t - 1 7t - 6t-1 7t j+ j+ cos t+ cos t+ 1 2 2 1 1 (Simplify your answers. Type exact answers.) -k -k= Di+Dj+k Find the domain of the following vector-valued function. r(t) = 81-i+ tj+ -k 2 2+t Select the correct choice below and fill in any answer boxes within your choice. OA. {t: t < OC. {t: ts or t OE. {t: sts } OG. {t: B. {t: t ort>} OD. {t: Consider the curve described by the following vector function. ) = (60e cost) i + (60e sint)j + (6 6e) k, for t0 a. What is the initial point of the path corresponding to r(0)? b. What is lim r(t)? t r c. Eliminate the parameter t to show that the curve r(t) lies on the surface z = 6 - 10' a. The initial point of the path corresponding to r(0) is (11). (Simplify your answer. Type integers or decimals.) where r = x + y.