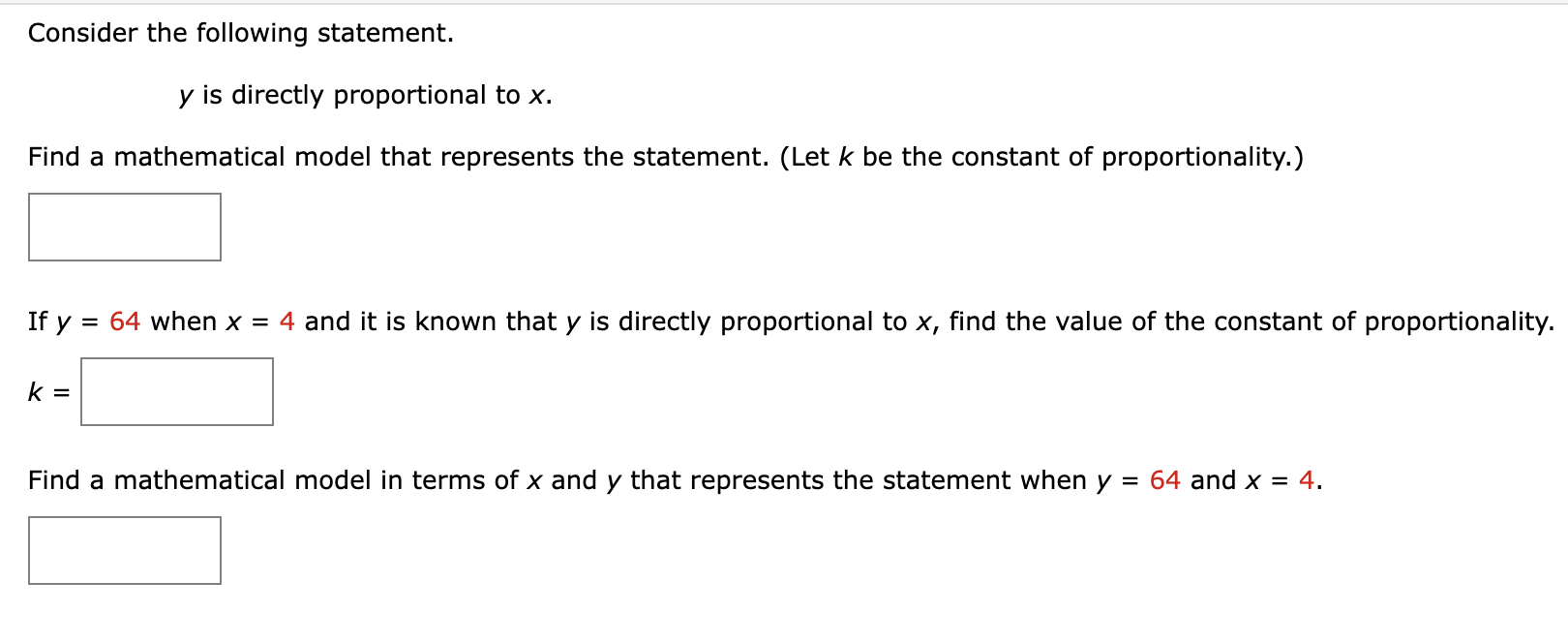
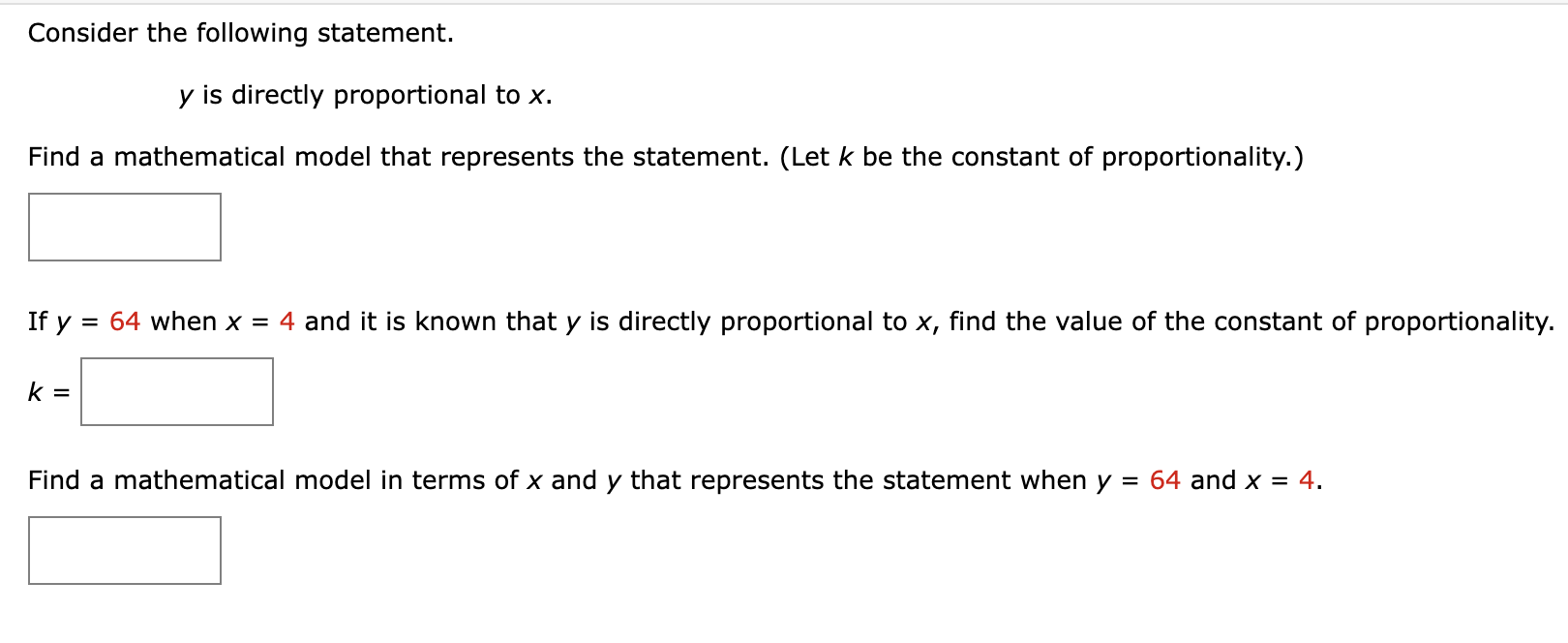
Find a mathematical model for the verbal statement. (Use k for the constant of proportionality.) h varies directly as the square root of s. S Find a mathematical model for the verbal statement. (Use k for the constant of proportionality.) z varies jointly as the quartic of x and the cube of y. S Find a mathematical model for the verbal statement. (Use k for the constant of proportionality.) The electric power P of a direct current circuit is jointly proportional to the voltage V and the electric current I. S Find a mathematical model for the verbal statement. (Use k for the constant of proportionality.) The gravitational attraction F between two objects of masses m1 and m2 is jointly proportional to the masses and inversely proportional to the square of the distance r between the objects. Find a mathematical model that represents the statement. (Determine the constant of proportionality.) P varies directly as x and inversely as the square of y. (P = E when x = 42 and y = 9.) E 3 Consider the following statement. y is directly proportional to x. Find a mathematical model that represents the statement. (Let k be the constant of proportionality.) S If y = 64 when X = 4 and it is known that y is directly proportional to x, find the value of the constant of proportionality. Find a mathematical model in terms of x and y that represents the statement when y = 64 and X = 4. E Consider the following statement. y varies inversely as x. Find a mathematical model that represents the statement. (Let k be the constant of proportionality.) S If y = 2 when x = 24 and it is known that y varies inversely as X, find the value of the constant of proportionality. Find a mathematical model in terms of x and y that represents the statement when y = 2 and x = 24. S Find a mathematical model that represents the statement. (Determine the constant of proportionality.) P varies directly as X and inversely as the square of y. (P = E when x = 42 and y = 6.) S 3 Find a mathematical model that represents the statement. (Determine the constant of proportionality.) z varies directly as the square of x and inversely as y. (z = 9 when x = 9 and y = 6.)