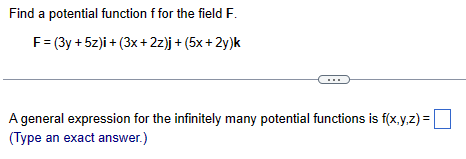
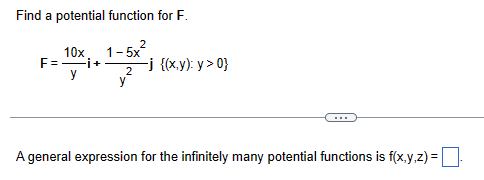
Find a potential function f for the field F. F = (3y + 5z)i + (3x + 2z)j + (5x + 2y)k A general expression for the infinitely many potential functions is f(x,y,z) = (Type an exact answer.)Find a potential function for F. 10x 1 -5x 2 F = + 2 i {(xy): y > 0} A general expression for the infinitely many potential functions is f(x,y,z) =Show that the differential form in the integral is exact. Then evaluate the integral. (1,2.3) 3x y dx + (x3- 6 j dy - 6yz dz (0,0,0) Compute the partial derivative.Although it is not defined on all of space R", the field associated with the line integral below is simply connected, and the component test can be used to show it is conservative. Find a potential function for the field and evaluate the integral. (3,5,3) 3z 18x dx + dy + 6z Iny dz (3,1,3) y A general expression for the infinitely many potential functions is f(x,y,z) =Although it is not defined on all of space R" , the field associated with the line integral below is simply connected, and the component test can be used to show it is conservative. Find a potential function for the field and evaluate the integral. (4,3.3) X Y dx + dy dz (2,3,2) y 7 2 Z A general expression for the infinitely many potential functions is f(x,y,z) =