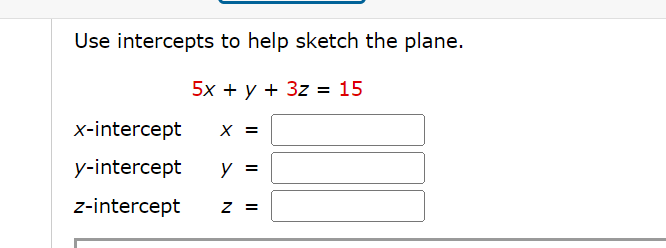
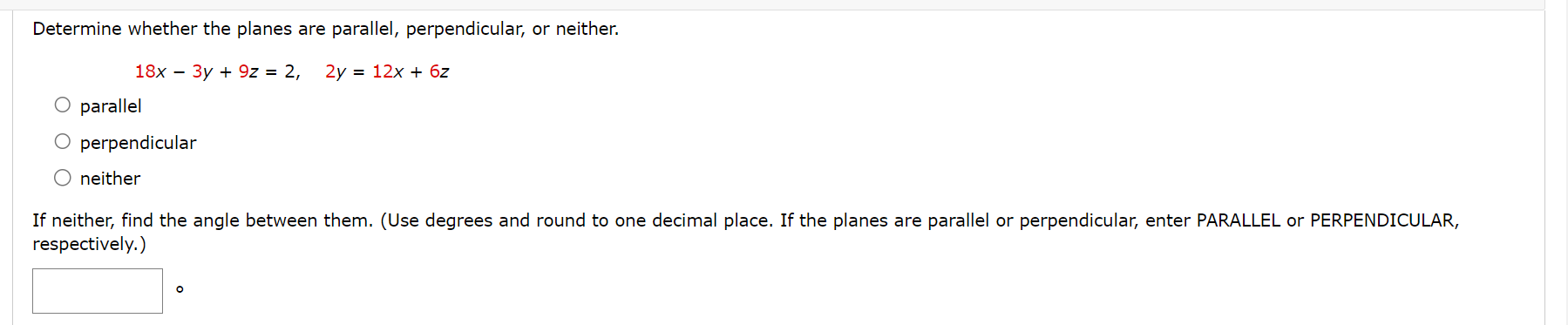
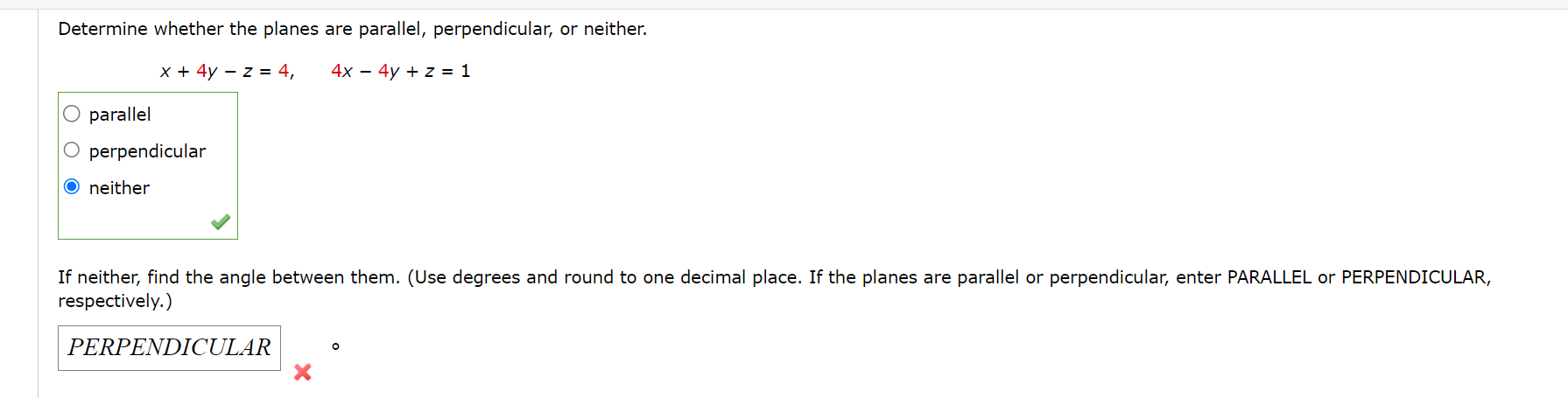
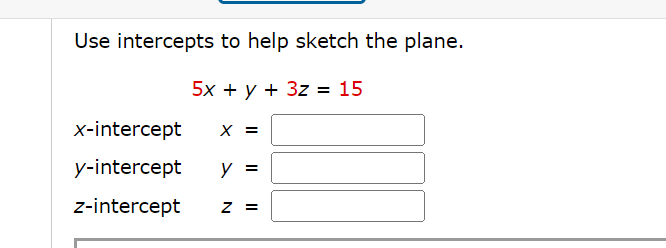
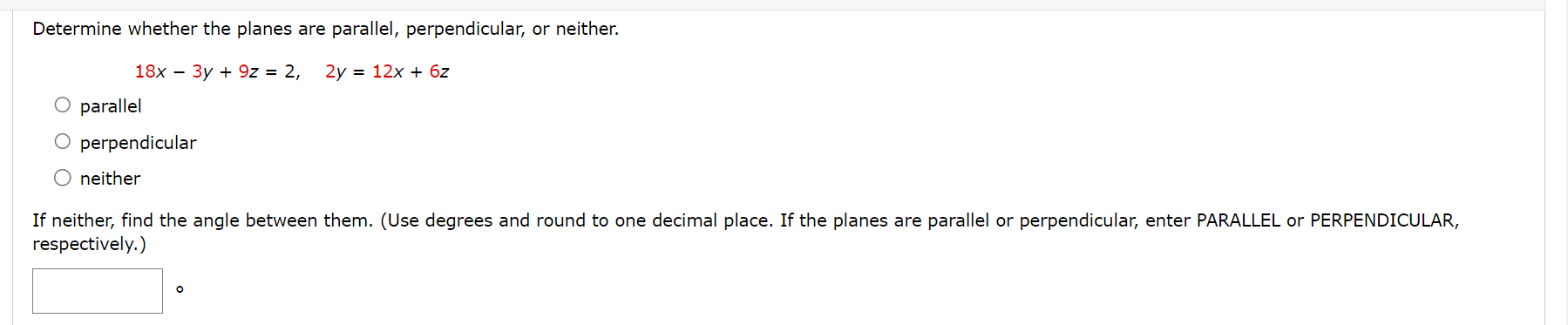
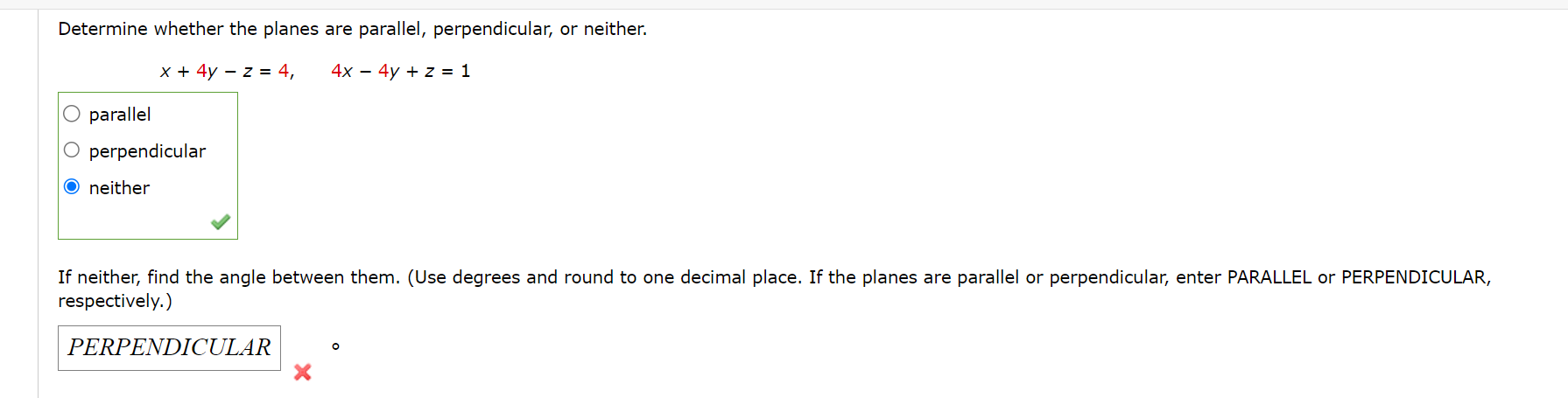
Find a vector equation and parametric equations for the line. (Use the parameter r.) The line through the point (5, 2.2, 3.6) and parallel to the vector 2i + 2j k r(t) = G -- I'v X (m), y(t), 2(0) =( 5 2:522 + 3:536 r ) v Find a vector equation and parametric equations for the line. (Use the parameter t. ) the line through the point (8, 0, -3) and parallel to the line x = 4 - 2t, y = -1 + 2t, z = 6 + 7t r(t) = (x (t ) , y (t), z(t ) ) =Is the line through (-4, 3, 0) and (1, 1, 1) perpendicular to the line through (2, 3, 4) and (5, -1, -7)? For the direction vectors of the lines, V1 . V2 = . Therefore, the lines are not v perpendicular.Find parametric equations for the line segment from (-3, 12, 32) to (11, -9, 45). (Use the parameter t.) x (t ) , y (t ), z(t ) ) =Find an equation of the plane. The plane through the point (6, 7, 2) and with normal vector 3i +j k Find an equation of the plane. the plane through the point (8, 3, 4) and parallel to the plane 2 = 4X 5y Find an equation of the plane. the plane that contains the line X = 2 + t, y = 4 t, z = 3 3t and is parallel to the plane 5X + 23/ + z = 4 Find an equation of the plane. The plane through the points (4, 1, 4), (5, 8, 6), and (4, 5, 1) Find an equation of the plane. the plane that passes through the point (4, 3, 2) and contains the line of intersection of the planes X + 2y + 32 = 1 and 2x y + z = 3 Find the point at which the line intersects the given plane. X=t1,y=1+2t, z=3t; 6Xy+52=9 (lerz)=( ) Determine whether the planes are parallel, perpendicular, or neither. 18X3y+92= 2, 2y: 12X+62 0 parallel O perpendicular O neither If neither, find the angle between them. (Use degrees and round to one decimal place. If the planes are parallel or perpendicular, enter PARALLEL or PERPENDICULAR, respectively.) Determine whether the planes are parallel, perpendicular, or neither. x + 4y - z = 4, 4x - 4y + z = 1 O parallel O perpendicular O neither If neither, find the angle between them. (Use degrees and round to one decimal place. If the planes are parallel or perpendicular, enter PARALLEL or PERPENDICULAR, respectively.) PERPENDICULAR XConsider the following planes. 5x4y+z= 1, 4x+y52=5 (a) Find parametric equations for the line of intersection of the planes. (Use the parameter 1".) (x(t), y(t). 2(0) = ( ) (b) Find the angle between the planes. (Round your answer to one decimal place.) :i" Find parametric equations for the line through the point (0, 2, 2) that is parallel to the plane x + y + z = 5 and perpendicular to the line x = 1 + t, y = 2 - t, z = 2t. (Use the parameter t.) ( x (t ) , y (t ) , z(t) ) =