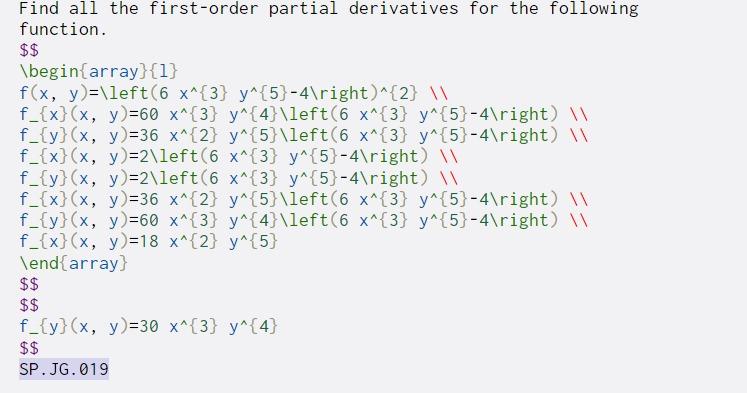
Find all the first-order partial derivatives for the following function. $$ \begin{array}{1} f(x, y)=\left(6 X^{3} y^{5}-4 ight)^{2} \ f_{x} (x, y)=60 X^{3} y^{4}\left(6 x^{3} y^{5}-4 ight) f_{y} (x, y)=36 x^{2} y^{5}\left(6 x^{3} y^{5}-4 ight) f_{x}(x, y)=2\left(6 X^{3} y^{5}-4 ight) f_{y} (x, y)=2\left(6 x^{3} y^{5}-4 ight) W f_{x}(x, y)=36 x^{2} y^{5}\left(6 x^{3} y^{5}-4 ight) f_{y}(x, y)=60 X^{3} y^{4}\left(6 x^{3} y^{5}-4 ight) W f_{x}(x, y)=18 X^{2} y^{5} \end{array} $$ $$ f_{y}(x, y)=30 X^{3} y^{4} $$ SP.JG.019