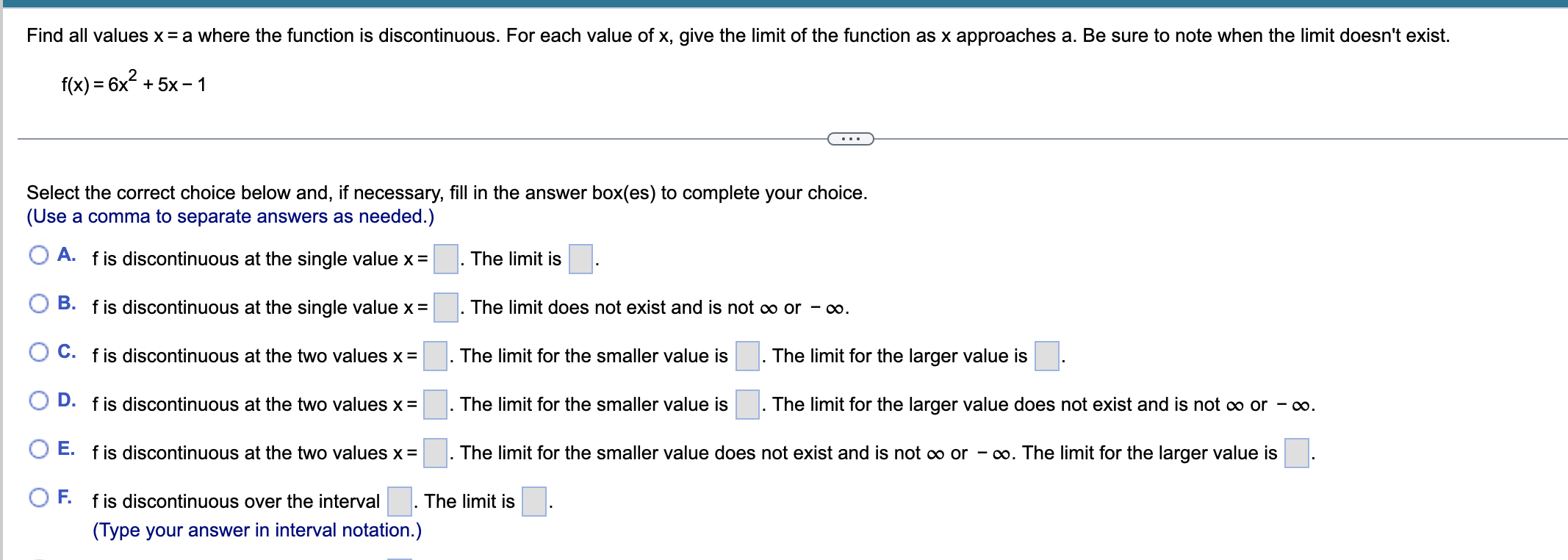
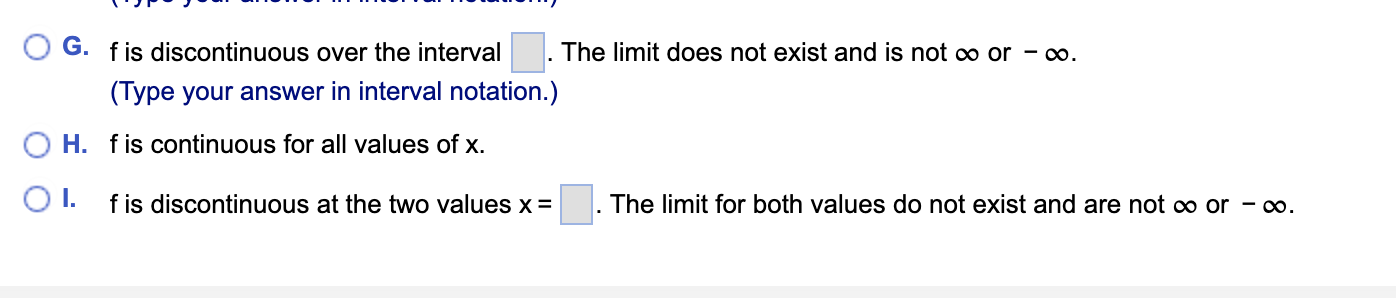
Find all values x = a where the function is discontinuous. For each value of x, give the limit of the function as x approaches a. Be sure to note when the limit doesn't exist. 8 +x f(x) = X(X - 2) Select the choice below and, if necessary, fill in the answer box(es) within your choice. (Use a comma to separate answers as needed.) O A. The function f is discontinuous at the single value x = . The limit is O B. The function f is discontinuous at the single value x = The limit does not exist and is not co or - co. O C. The function f is discontinuous at the two values x = The limit for the smaller value is . The limit for the larger value is O D. The function f is discontinuous at the two values x = The limit for the smaller value is . The limit for the larger value does not exist and is not co or - co. O E. The function f is discontinuous at the two values x = The limit for the smaller value does not exist and is not co or - co. The limit for the larger value is O F. The function f is discontinuous over the interval . The limit is (Type your answer in interval notation.)O G. The function f is discontinuous over the interval The limit does not exist and is not co or - co. (Type your answer in interval notation.) O H. The function f is continuous for all values of x. O I. The function f is discontinuous at the two values x = The limits for both values do not exist and are not co or - co.Find all values x = a where the function is discontinuous. For each value of x, give the limit of the function as x approaches a. Be sure to note when the limit doesn't exist. f(x) = 6x4+ 5x -1 . . . Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. (Use a comma to separate answers as needed.) O A. f is discontinuous at the single value x = The limit is O B. f is discontinuous at the single value x = The limit does not exist and is not co or - co. O C. f is discontinuous at the two values x = The limit for the smaller value is The limit for the larger value is O D. f is discontinuous at the two values x = The limit for the smaller value is . The limit for the larger value does not exist and is not co or - co. O E. f is discontinuous at the two values x = . The limit for the smaller value does not exist and is not co or - co. The limit for the larger value is O F. f is discontinuous over the interval . The limit is (Type your answer in interval notation.)O G. f is discontinuous over the interval The limit does not exist and is not co or - co. (Type your answer in interval notation.) O H. f is continuous for all values of X. O I. f is discontinuous at the two values x = The limit for both values do not exist and are not co or - co.Find all values x = a where the function is discontinuous. For each value of x, give the limit of the function as x approaches a. Be sure to note when the limit doesn't exist. k (x ) = e V x -3 . . . Select the correct choice below and, if necessary, fill in the answer box(es) within your choice. (Use a comma to separate answers as needed.) O A. f is discontinuous at the single value x = The limit is O B. f is discontinuous at the single value x = . The limit does not exist and is not co or - co. O C. f is discontinuous at the two values x = The limit for the smaller value is The limit for the larger value is O D. f is discontinuous at the two values x = The limit for the smaller value is . The limit for the larger value does not exist and is not co or - co. O E. f is discontinuous at the two values x = The limit for the smaller value does not exist and is not co or - co. The limit for the larger value is O F. f is discontinuous over the interval . The limit is (Type your answer in interval notation.)- f is discontinuous over the interval . The limit does not exist and is not 00 or - co. (Type your answer in interval notation.) f is continuous for all values of x. f is discontinuous at the two values x = . The limits for both values do not exist and are not 00 or - oo. a) Find lim C(x). Select the correct choice below and ll in any answer boxes in your choice. x>3 if} A- lim C(x) = $ (Type an integer or a decimal.) x>3 {I} B. The limit does not exist. b) Find lim C(x). Select the correct choice below and fill in any answer boxes in your choice. X-3+ O A. lim C(x) = $ (Type an integer or a decimal.) X- 3+ O B. The limit does not exist.c) Find lim C(x). Select the correct choice below and fill in any answer boxes in your choice. x>3 5:? A- lim C(x) = $ (Type an integer or a decimal.) x>3 {I} B. The limit does not exist. d) Find C(3). Select the correct choice below and fill in any answer boxes in your choice. O A. C(3) = $ (Type an integer or a decimal.) O B. The solution is undefined.e) Find all values on the interval (0,4) where the function is discontinuous. D (Use a comma to separate answers as needed.) First-class postage is $0.31 for the rst ounce (or any fraction thereof) and $0.23 for each additional ounce (or fraction thereof). Let C(x) represent the postage for a letter weighing x oz. Use this information to answer the questions