Find f'(x) for f(x) = 2x + 3x - 1. Be sure to use f'(x) = lim BH to get credit. or f'(x) =
![( lim _{x ightarrow frac{1}{2}^{+}}left[x tan pi x+ln left(x-frac{1}{2}ight)ight] )](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2023/02/63ef10370f590_1676612014388.png)
![18. (BONUS, 5 pts) Find ( f^{prime}(x) ) for ( f(x)=sqrt[3]{x} ). Be sure to use ( f^{prime}(x)=lim _{b ightarrow](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2023/02/63ef10370ca48_1676612014260.png)
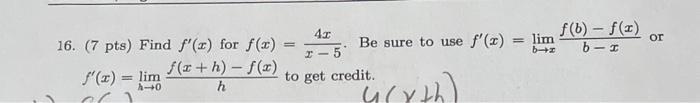
Find f'(x) for f(x) = 2x + 3x - 1. Be sure to use f'(x) = lim BH to get credit. or f'(x) = lim A-0 f(x+h)-f(x) h f(b)-f(x) b-I Find the limit lim 1+ H4 2 a (x - )]. 2 x tan x + ln 18. (BONUS, 5 pts) Find f'(x) for f(x)=x. Be sure to use f'(x) = lim f(b) = f(x) bir to get credit. or f'(x) = lim h0 f(a+h)-f(x) h 16. (7 pts) Find f'(x) for f(x) f(x+h)-f(x) h f'(x) = lim CC 4x I- 5 to get credit. = f(b)-f(x) or Be sure to use f'(x) = lim: (4(x+h) bx bIH Use the e- & definition to prove that lim(3x + 7) = 22. x15 Use the e-6 definition to prove that lim (x - 1) = 63. 1-8
Step by Step Solution
3.52 Rating (172 Votes )
There are 3 Steps involved in it
Step: 1
Absolutely lets find the derivative of the function fx 22 3x 1 According to the limit definition of the derivative fx is represented by fx limh 0 fx h fx h Here fx 22 3x 1 Lets substitute this functio...
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2
Step: 3
Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started
Authors: Ron Larson
10th edition
9781337514255, 1337271179, 133751425X, 978-1337271172
