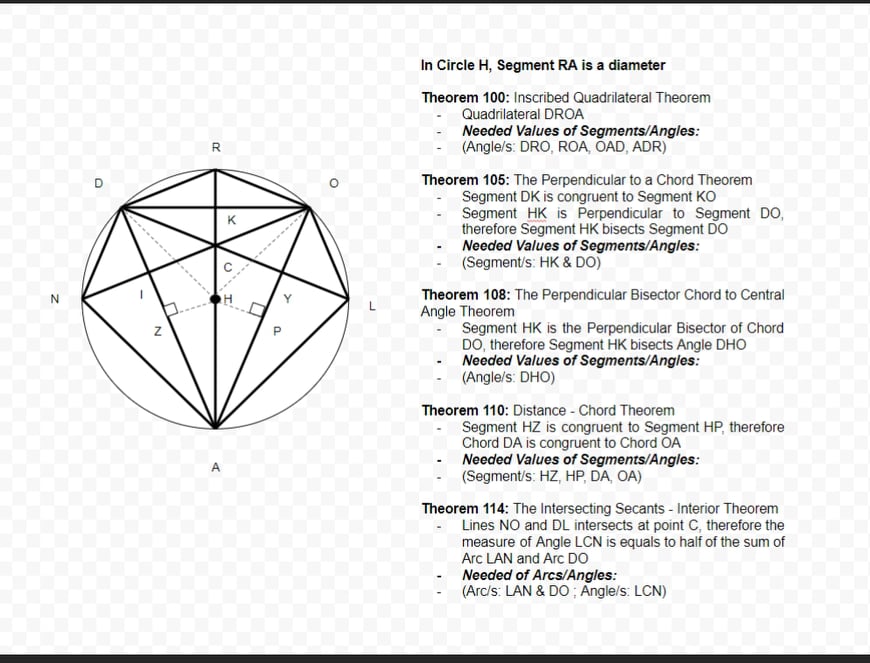
Question: Find the angle and segment with solutions. You may create your own values. Note: Theorem 110, must have special right triangle to prove. In Circle
Find the angle and segment with solutions. You may create your own values.
Note: Theorem 110, must have special right triangle to prove.
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


