Question: Find the approximate minimum surface area of an open rectangular box (with no top}, with a square base 3: cm by .1: cm and height

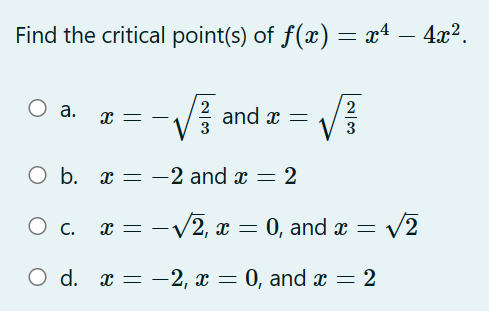


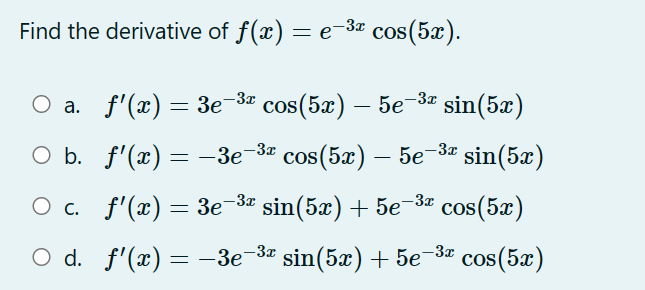



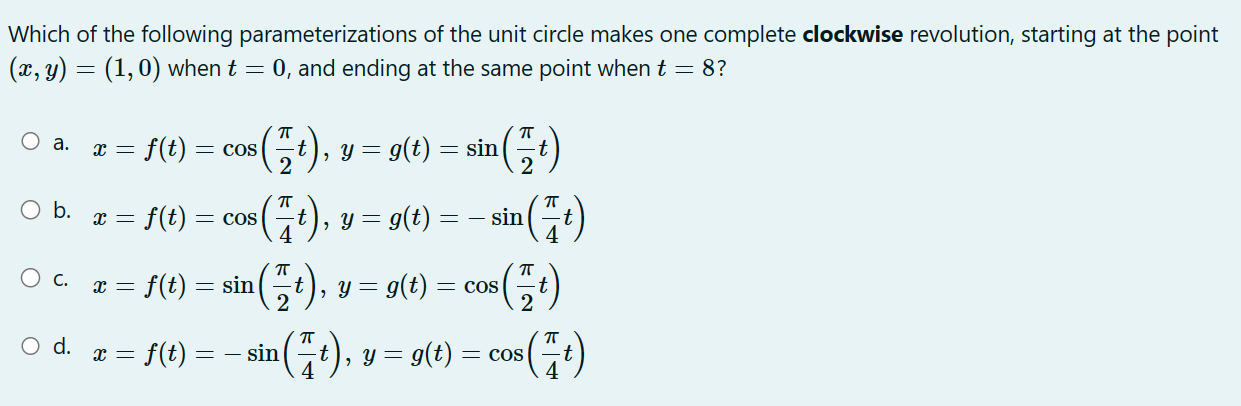

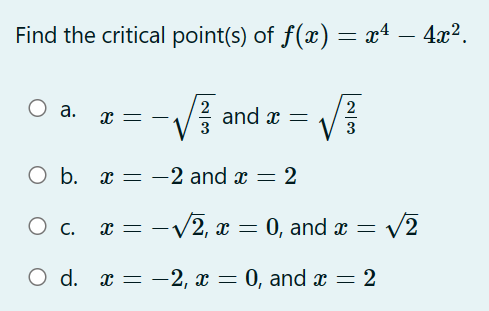


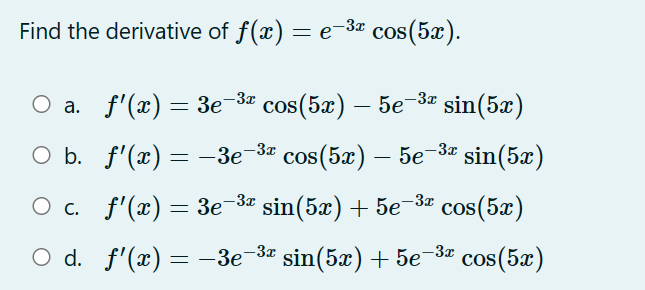
![and bounded interval [5, 2] (that is, for 5 g a: g](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6660e37c18145_7246660e37c076e4.jpg)

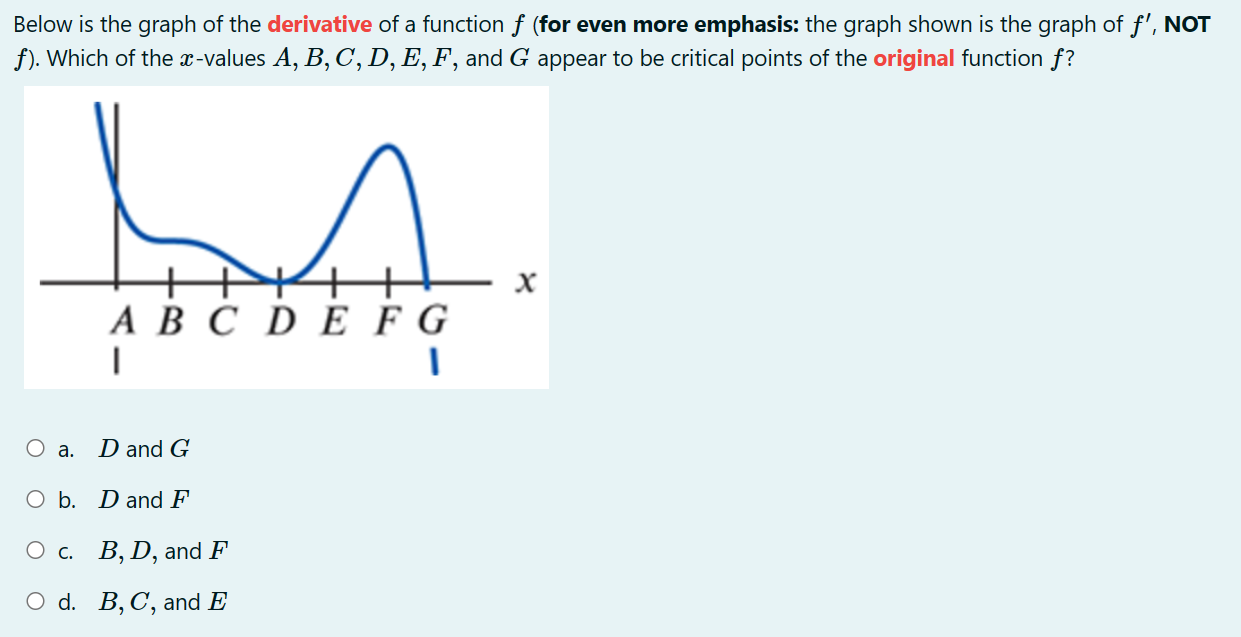

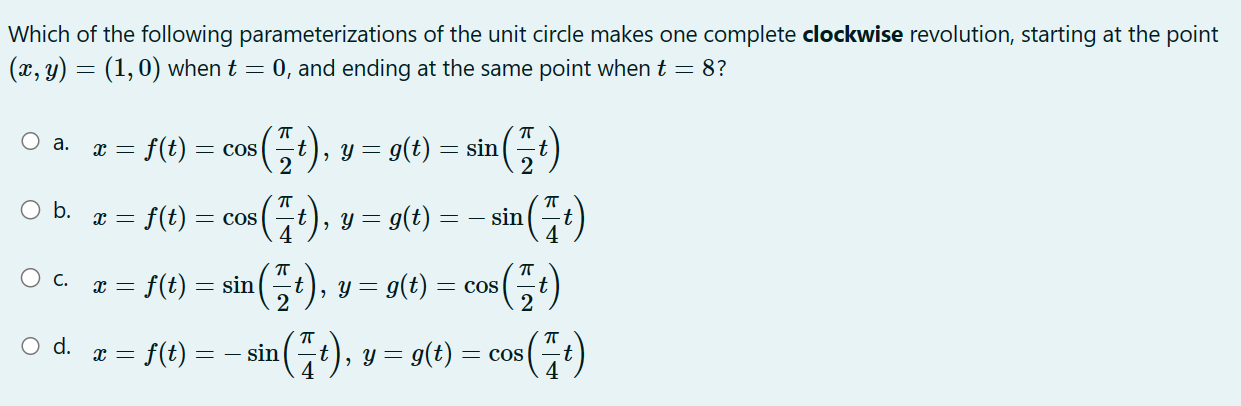
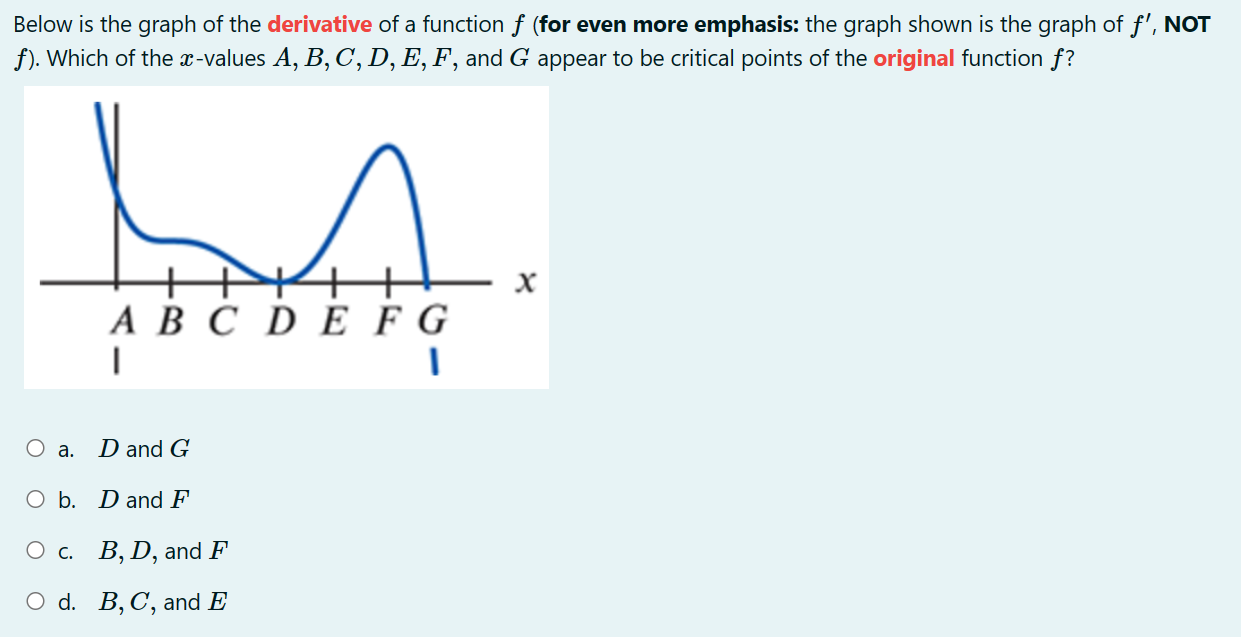
Find the approximate minimum surface area of an open rectangular box (with no top}, with a square base 3: cm by .1: cm and height h cm whose volume is 200 (3mg. 0 a. approximately 205.197 cm2 0 b. approximately 162.865 cm2 0 c. approximately 128.445 cm2 0 d. approximately 217.153 cm2 Consider the one-parameter family of functions fa (x ) = ax - vac for x 2 0 and a > 0. Find the value of a > 0 so that a critical point of fa (x ) occurs at x O a. a = Ob. a= 4 O C. a = O d. a =3A right triangle has one leg of length 12 cm. How fast is the area changing at the instant that the other leg has a length of 15 cm and is increasing at 4 cm per second? 0 a. 30 cm2 /sec 0 b. 24 cm2 /sec 0 c. 48 cm2 /sec 0 d. 12cm2/sec Find the global (or "absolute") minimum value (output) of w) : $4 18w2 + 10 over the closed and bounded interval [5, 2] (that is, for 5 g a: g 2). O a. 185 O b. 10 O c. 46 0 d. 771 An automobile purchased in 2020 has a value which is approximated by the function V(t) : 35(087)', where t is time, in years from the data of purchase, and V(t) is the value, in thousands of dollars. Find V'(4), including units. 0 a. 71.8 thousand dollars per year 0 b. 2.8 thousand dollars per year 0 c. 1.4 thousand dollars per year 0 d. 72.1 thousand dollars per year Below is the graph of the derivative of a function f {for even more emphasis: the graph shown is the graph of f', NOT f). Which of the mvalues A, B, C, D, E, F, and G appear to be critical points of the original function f? ABCDEFG O a. D and G O b. D and F O c. B, D, and F 0 d. B, C, and E Find the tangent line approximation (local linearization) to f(a) = near * = 2. O a. x for x ~ 2 O b. 1 (a - 2) for a ~ 2 O C. 1 (x - 2) for x ~ 2 O d. 1 - x for x ~ 2 x2 4Which of the following parameterizations of the unit circle makes one complete clockwise revolution, starting at the point (x, y) = (1,0) when t = 0, and ending at the same point when t = 8? O a. x = f(t) = cos "t ) , y = g(t) = sin t Ob. x = f(t) = cos (_t) , y = g(t) = - sin( # t) Oc. x =f(t) = sin ,t ) , y = g (t ) = cos t Od. x = f (t) - - sin ("t), y = g(t) = cos(#t)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


