Find the average value of the function

f(x)=5+x^(2)

on the interval

-2,4

.\ Solution\ With

a=-2

and

b=4

, we have\

f_(ave )=(1)/(b-a)\\\\int_a^b f(x)dx\ =(1)/((4-()\\\\int_(-2)^4 (5+x^(2))dx

))

\ =

[

]_(-2)^(4)\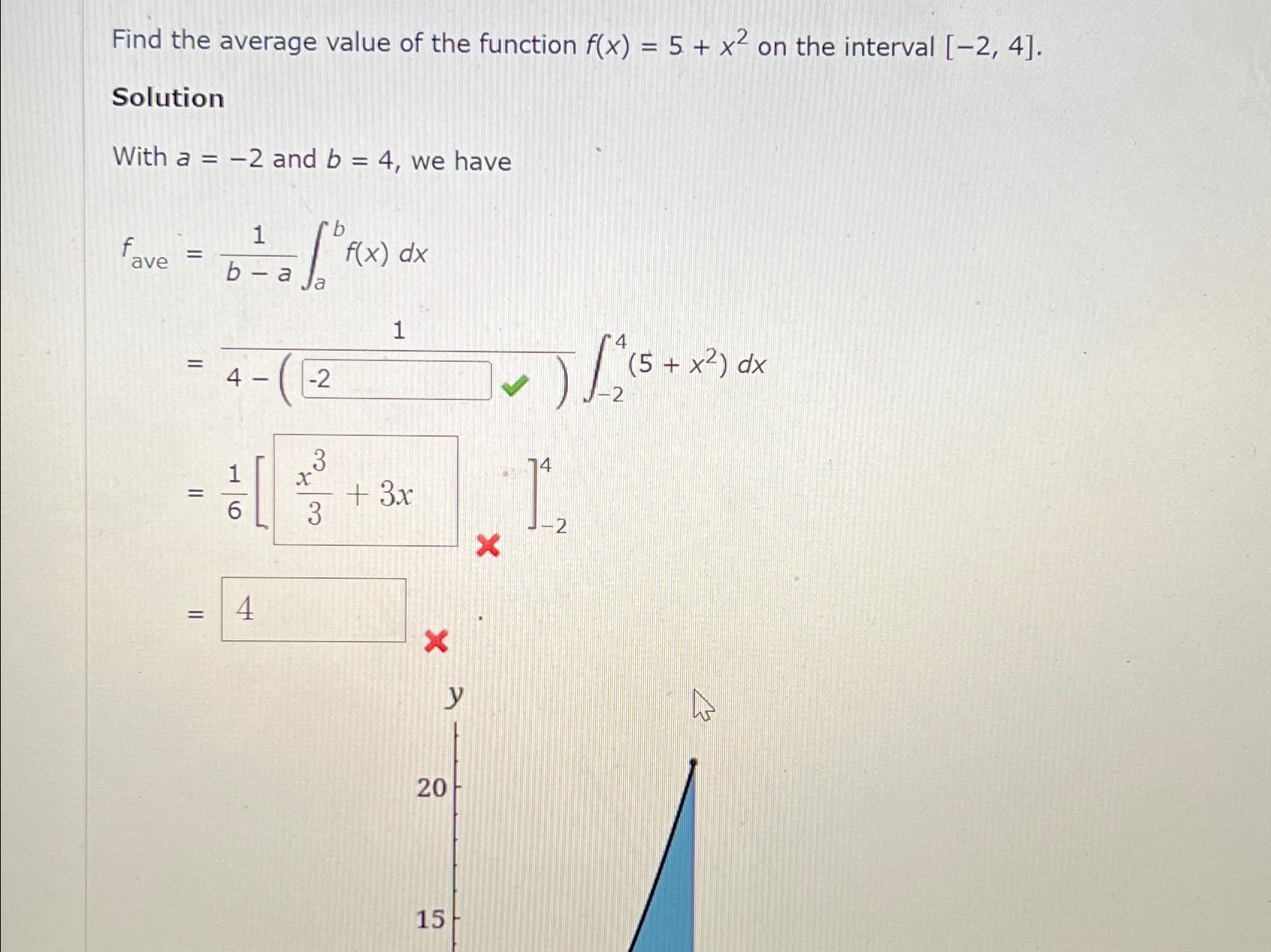

Find the average value of the function f(x)=5+x2 on the interval [2,4]. Solution With a=2 and b=4, we have fave=ba1abf(x)dx=4(124(5+x2)dx=61[3x3+3x