Find the component form of the unit vector that makes an angle 0 = 3 with the positive x-axis. The component form of the vector

Question

25 users unlocked this solution today!

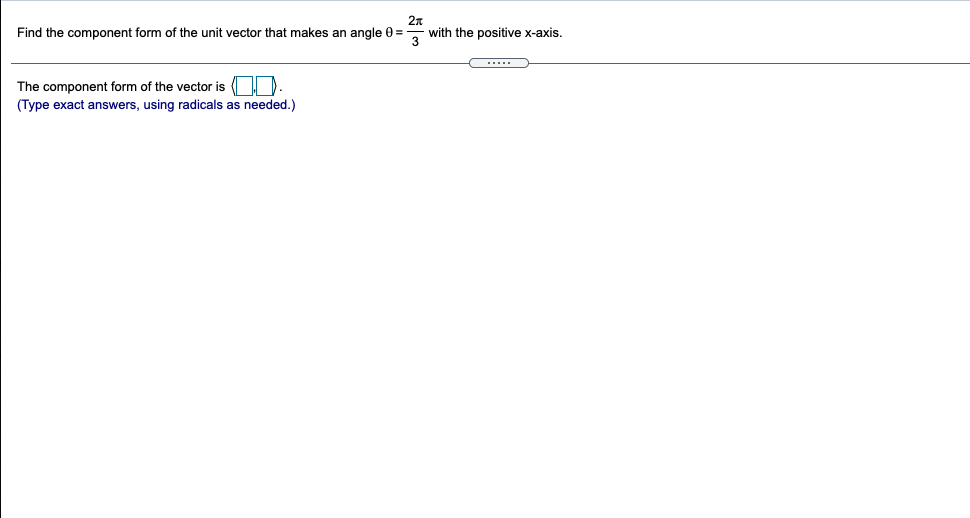
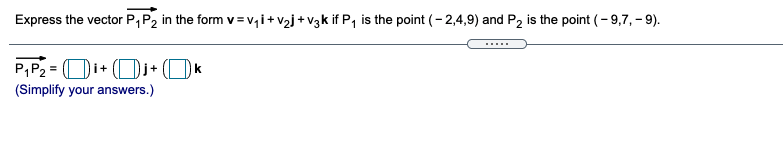
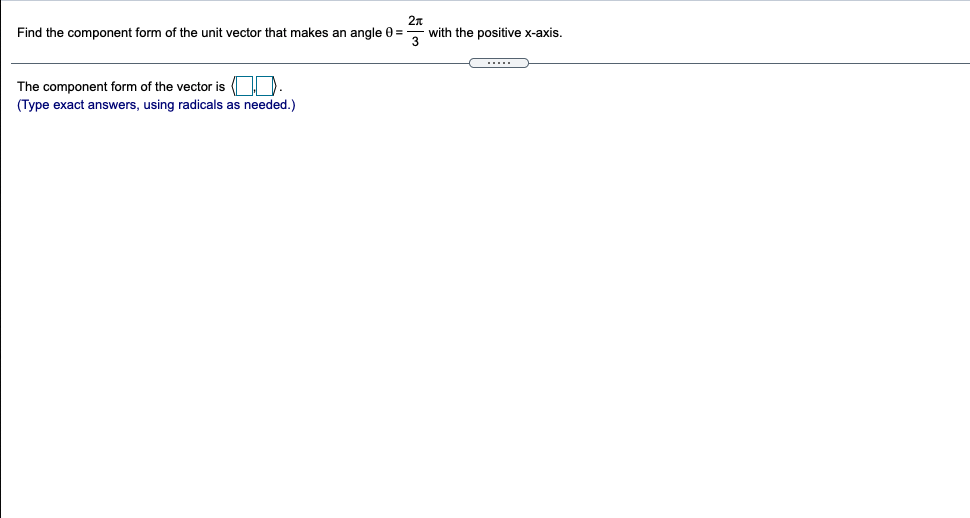
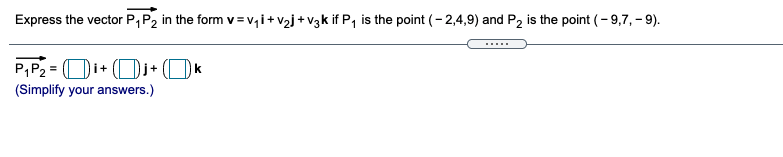
Find the component form of the unit vector that makes an angle 0 = 3 with the positive x-axis. The component form of the vector is( (Type exact answers, using radicals as needed.)Find the component form of the unit vector obtained by rotating the vector (0,1) 210" counterclockwise about the origin. Choose the correct answer below. O A. 13 O B. 1/2 2 ' 2 2 2 O C. 12 12 OD. 1 2 2 2' 2 OE. OF. 2 2 2 '2Express the vector P, P, in the form v = vi + v2j + vak if P, is the point ( - 2,4,9) and P2 is the point ( - 9,7, - 9). P1 P2 = ( Di+ (D) )+ (Simplify your answers.)Express the vector in the form v = v, i + vaj + V3k. AB if A is the point (10, - 4,5) and B is the point (7, - 4,1) Choose the correct answer below. O A. 171-8j+6k O B. 11i+4k O C. - 111-4k O D. -31-4k O E. - 171+8j -6k OF. 31+4kExpress the following vector in the form v = v, i + voj + vgk. 3u - v if u = (6,5, -7) and v = (8, - 5,1) 3u - V= K (Simplify your answers.)