Consider the circuit below. The battery has an emf of = 30.00 V and an internal resistance of r = 1.00 (a) Find

Consider the circuit below. The battery has an emf of

ε = 30.00 V

and an internal resistance of

r = 1.00 Ω

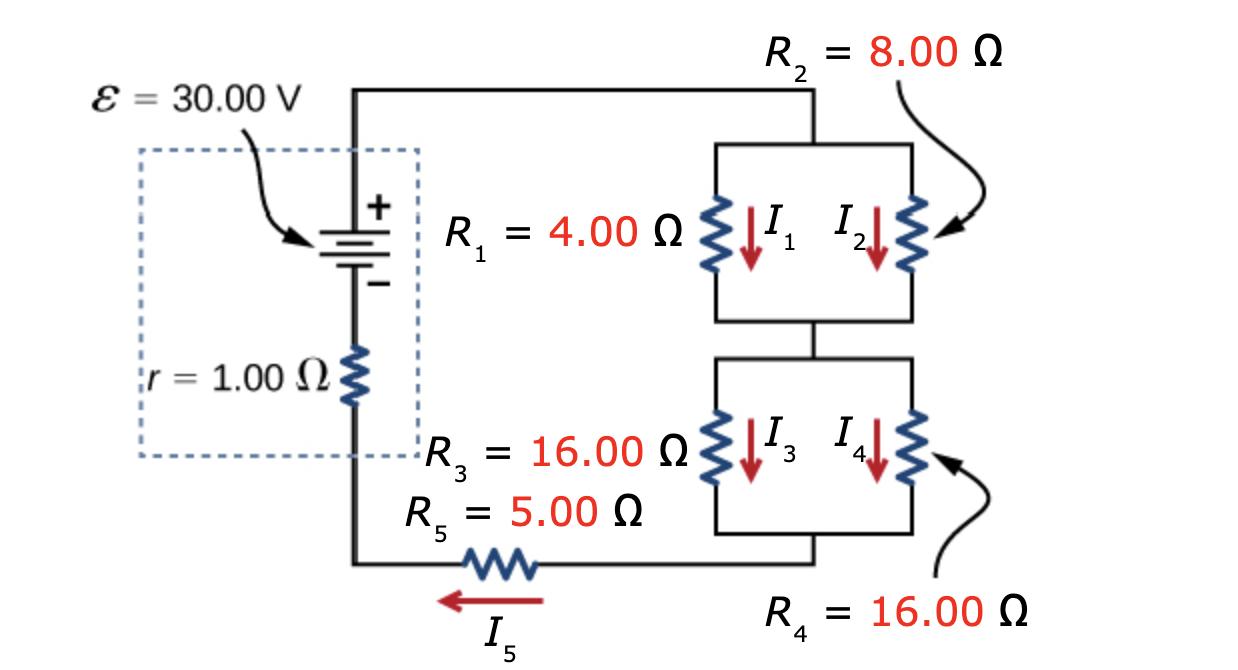
(a) Find the equivalent resistance of the circuit (in Ω) and the current out of the battery (in A). (For the current, indicate the direction with the sign of your answer.) Req = Ω I = A

(b) Find the current (in A) through each resistor. (Indicate the direction with the signs of your answers. Assume the positive direction of the current through the internal resistor is upward.) I1 = A I2 = A I3 = A I4 = A I5 = A Ir = A

(c) Find the potential drop (in V) across each resistor. V1 = V V2 = V V3 = V V4 = V V5 = V Vr = V

(d) Find the power (in W) dissipated by each resistor. P1 = W P2 = W P3 = W P4 = W P5 = W Pr = W

(e) Find the total power (in W) supplied by the batteries. W

= 8.00 N E = 30.00 V + R, = 4.00 0SI. 1 ir = 1.00 2 0S I, I, R = 16.00 3 R, = = 5.00 Q %3D R, = 16.000 I 5 4