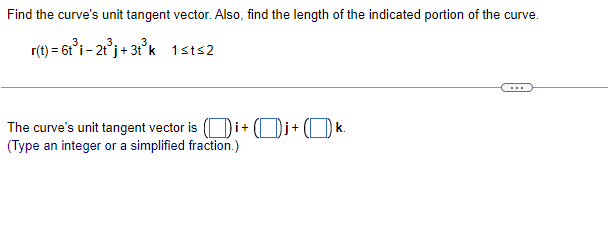
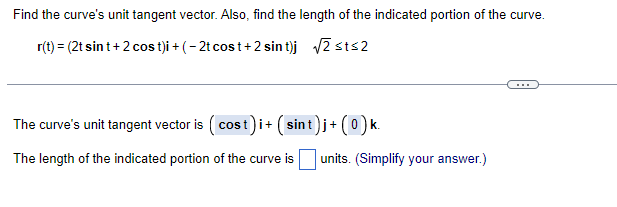
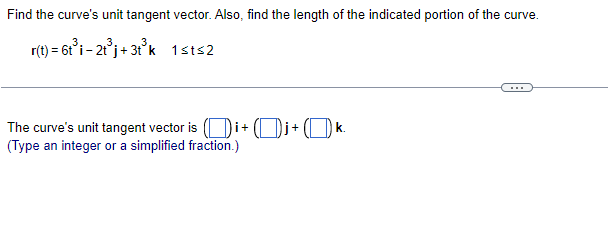
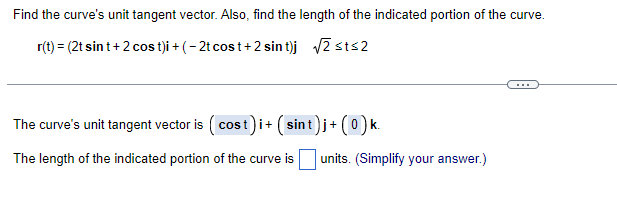
Find the curve's unit tangent vector. Also, find the length of the indicated portion of the curve. r(t) = (cost)i+ (sint) k, osts Find the curve's unit tangent vector. T(t) = kFind the curve's unit tangent vector. Also, find the length of the indicated portion of the curve. r(t) = 6ti- 2+3 2t j + 3t k 1st=2 The curve's unit tangent vector is i + + K (Type an integer or a simplified fraction.)Find the curve's unit tangent vector. Also, find the length of the indicated portion of the curve. r(t) = (2t sint + 2 cost)i + ( -2t cost + 2 sint)j #2 sts2 The curve's unit tangent vector is ( cost) i+ ( sint)j + (0)k- The length of the indicated portion of the curve is units. (Simplify your answer.)