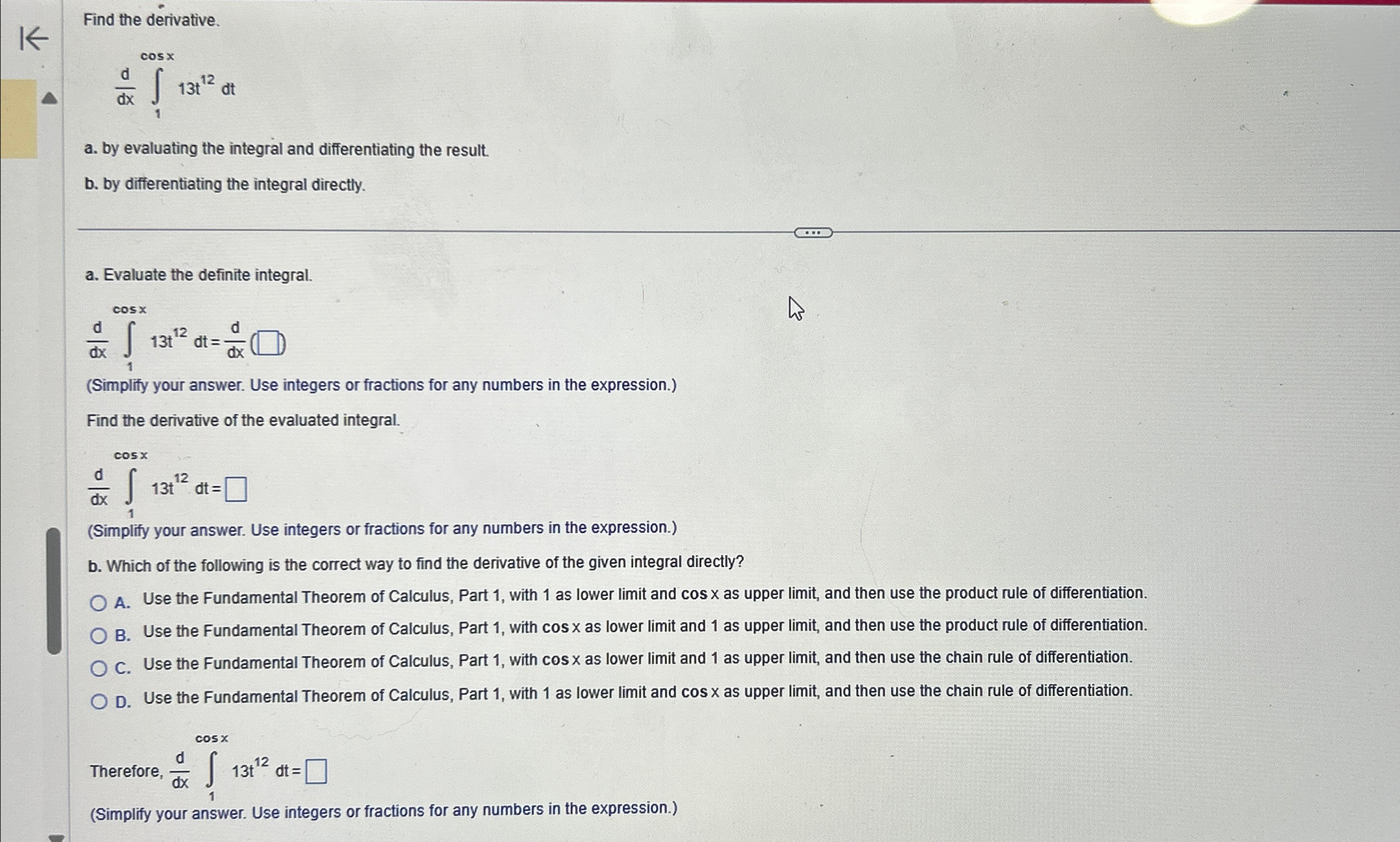
Question: Find the derivative. d d x 1 c o s x 1 3 t 1 2 d t a . by evaluating the integral and
Find the derivative.
a by evaluating the integral and differentiating the result.
b by differentiating the integral directly.
a Evaluate the definite integral.
Simplify your answer. Use integers or fractions for any numbers in the expression.
Find the derivative of the evaluated integral.
Simplify your answer. Use integers or fractions for any numbers in the expression.
b Which of the following is the correct way to find the derivative of the given integral directly?
A Use the Fundamental Theorem of Calculus, Part with as lower limit and as upper limit and then use the product rule of differentiation.
B Use the Fundamental Theorem of Calculus, Part with as lower limit and as upper limit and then use the product rule of differentiation.
C Use the Fundamental Theorem of Calculus, Part with as lower limit and as upper limit and then use the chain rule of differentiation.
D Use the Fundamental Theorem of Calculus, Part with as lower limit and as upper limit and then use the chain rule of differentiation.
Therefore,
Simplify your answer. Use integers or fractions for any numbers in the expression.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


