Question: Find the directions in the tog-plane in which the function fit-:3} = E 3x2 25:? has zero change at the point P[1.1 .1). Express the
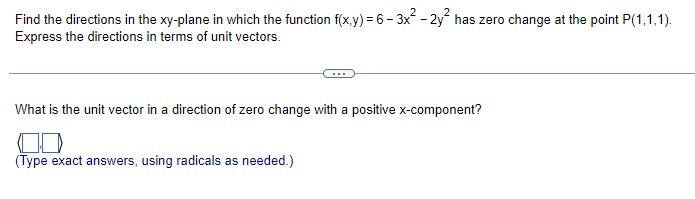



![fin-L311] 4 Extra: the point P{ 1: 1,1]: and the unit vector](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666198bd102b5_125666198bd02196.jpg)


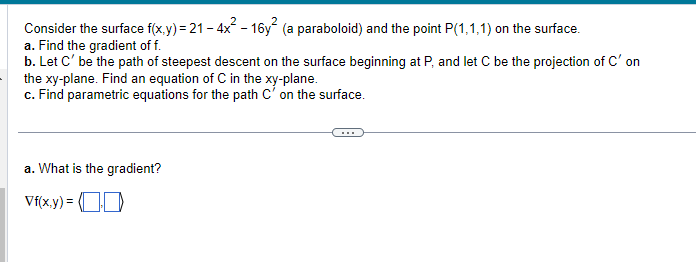

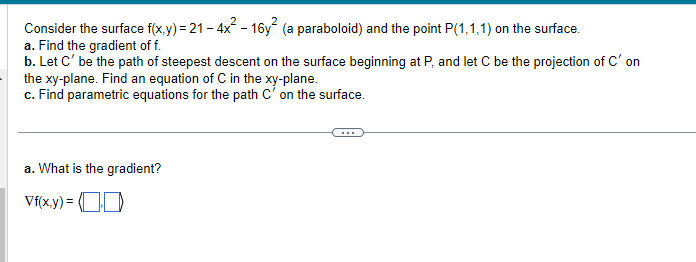
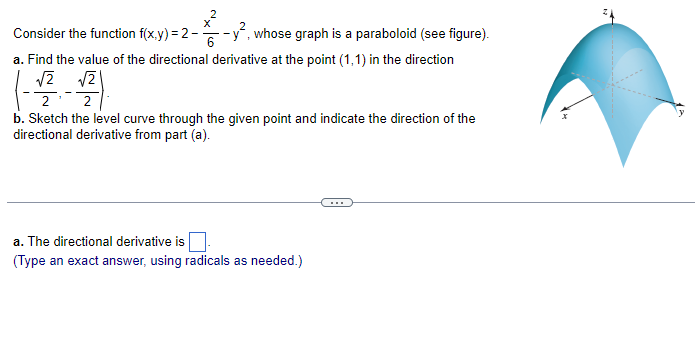
Find the directions in the tog-plane in which the function fit-:3} = E 3x2 25:? has zero change at the point P[1.1 .1). Express the directions in terms of unit vectors. What is the unit vector in a direction of zero change I.Irith a positive x-component'? {DD [Type exact answers. using radicals as needed.) 1 1 1 . - : + - _ _ ' : __ _ _ Considerthe function fin-L311] 4 Extra: the point P{ 1: 1,1]: and the unit vector u ( E , 4E , E D. a. Compute the gradient off and evaluate it at P. b. Find the unit vector in the direction of maximum increase off at P. c. Find the rate of change of the function in the direction of maximum increase at P. :1. Find the directional derivative at P in the direction ofthe given vector. a. What is the gradient at the point [ 1: 1:1]? {DD-[i 1 1 Consider the function ix. .2 = 4x2 + 4 2 +422 +3. the oint P 1.113 . and the unit vector u = _g_ . iv) v . r:' t..]. did? a. Compute the gradient off and evaluate it at P. b. Find the unit vector in the direction of maximum increase off at P. c. Find the rate of change of the function in the direction of maximum increase at P. d. Find the directional derivative at F in the direction ofthe given vector. at. What is the gradient at the point [1 .13}? {DD-[i Consider the surface fig-c3) = 9 + x: {a plane] and the point Pl: 34:5]: on the surface. a. Find the gradient of f. b. Let C" be the path of steepest descent on the surface beginning at P: and let G be the projection of C" on the xiiplane. Find an equation of C in the Jarplane. c. Find parametric equations for the path C" on the surface. a. What is the gradient? area} = (DD 2 :1: Consider the function lift-:3} = 2 F 4'92: whose graph is a pa raboloid {see figure]. a. Find the value of the directional den'vative at the point (1.1] in the direction 4'? 4E ' T - ' T - b. Sketch the level curve through the given point and indicate the direction of the directional derivative from part [a]. <: a. the directional derivative is e. an exact answer: using radicals as needed>
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


