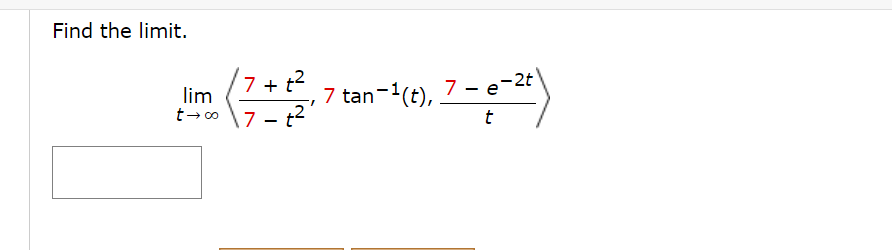
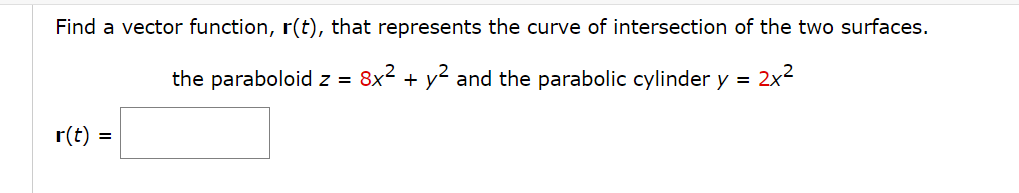
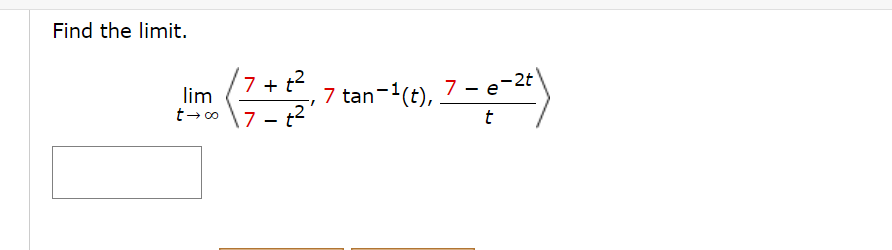
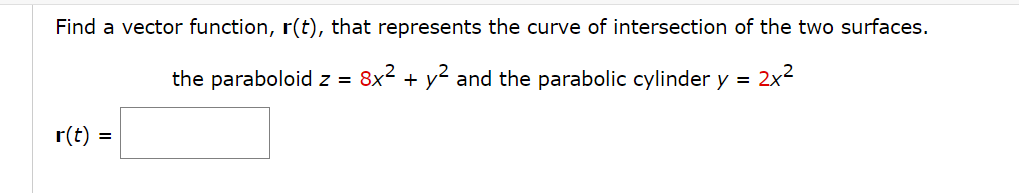
Find the domain of the vector function. (Enter your answer using interval notation.) 1 t8 r(t) = cos(t)i + |n(t)j + k S Sketch the curve with the given vector equation by finding the following points. (Select Update Graph to see your response plotted on the screen. Select the Submit button to grade your response.) r(t) = (t, 7 t, 2t) ( 77:14.7 14 ) X rm) (x, v.2) = ( ) r0) (x, y. z) = l l r(-7) (x, y. 2) At what points does the curve r(t) = ti + (3t - t=) k intersect the paraboloid z = x2 + 2? (smaller t-value) ( x, y, z ) = (larger t-value) ( x, y, Z) =Find a vector function, r(t), that represents the curve of intersection of the two surfaces. the paraboloid z = 8x2 + y2 and the parabolic cylinder y = 2x2 rm Find an equation of the sphere with center (1, 12, 6) and radius 10. Use an equation to describe its intersection with each of the coordinate pianes. (If the sphere does not intersect with the plane, enter DNE.) intersection with xy-plane 64 X intersection with xz-plane 4'1 X intersection with yzplane 99 Find an equation of the sphere that passes through the origin and whose center is (2, 1, 3). (x "2 i (y 1)2: (2 3)2:14