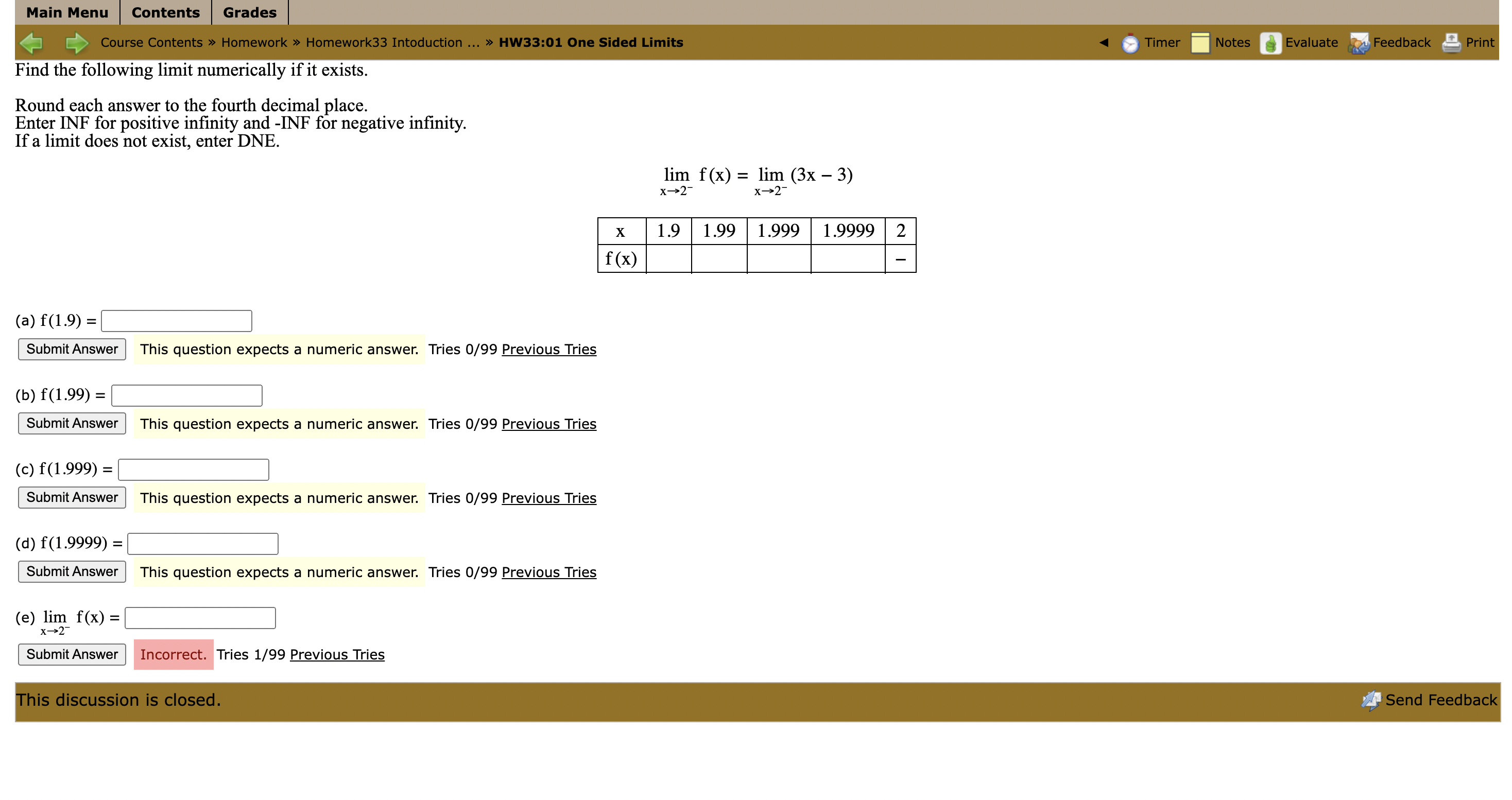
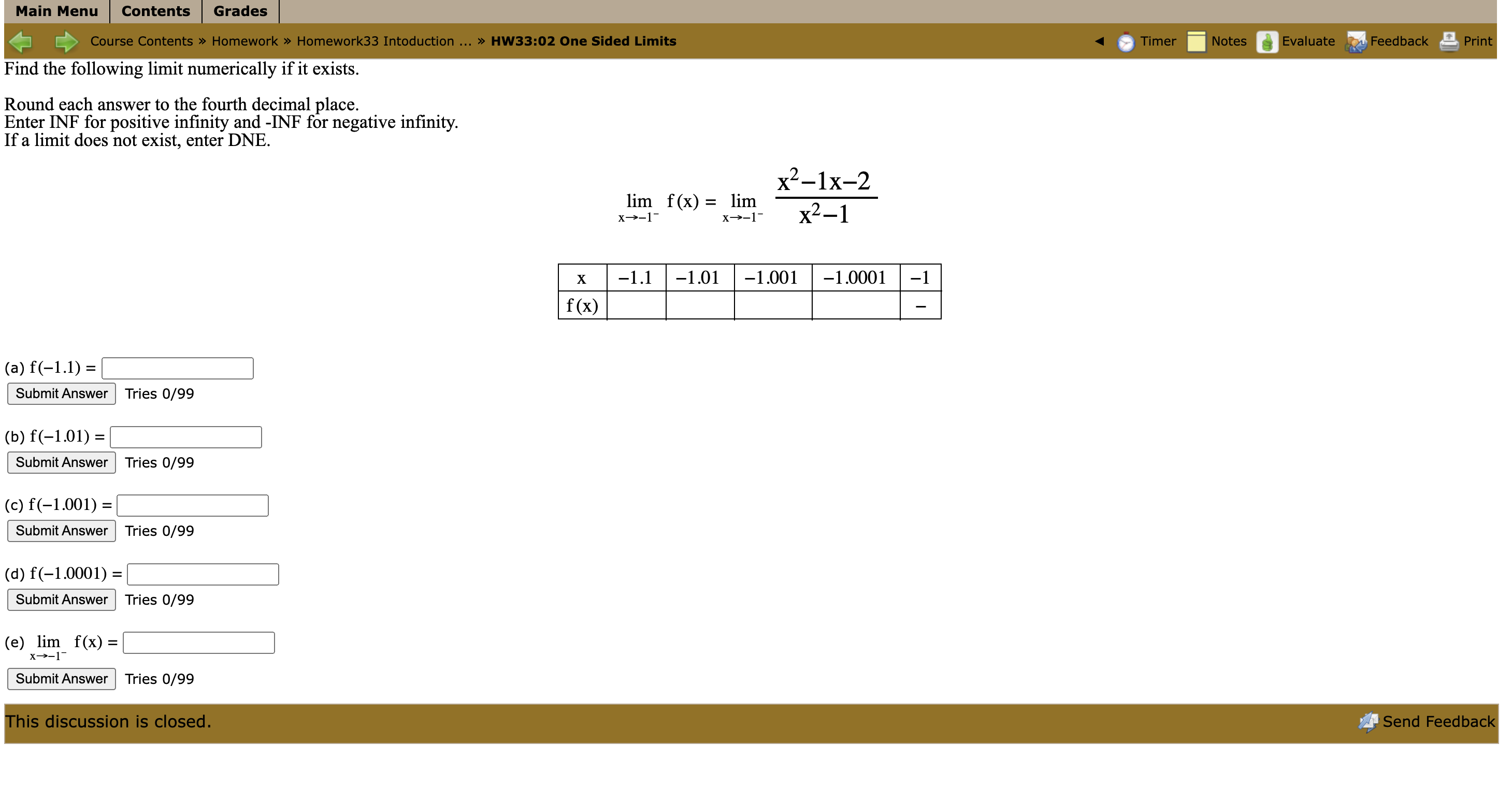
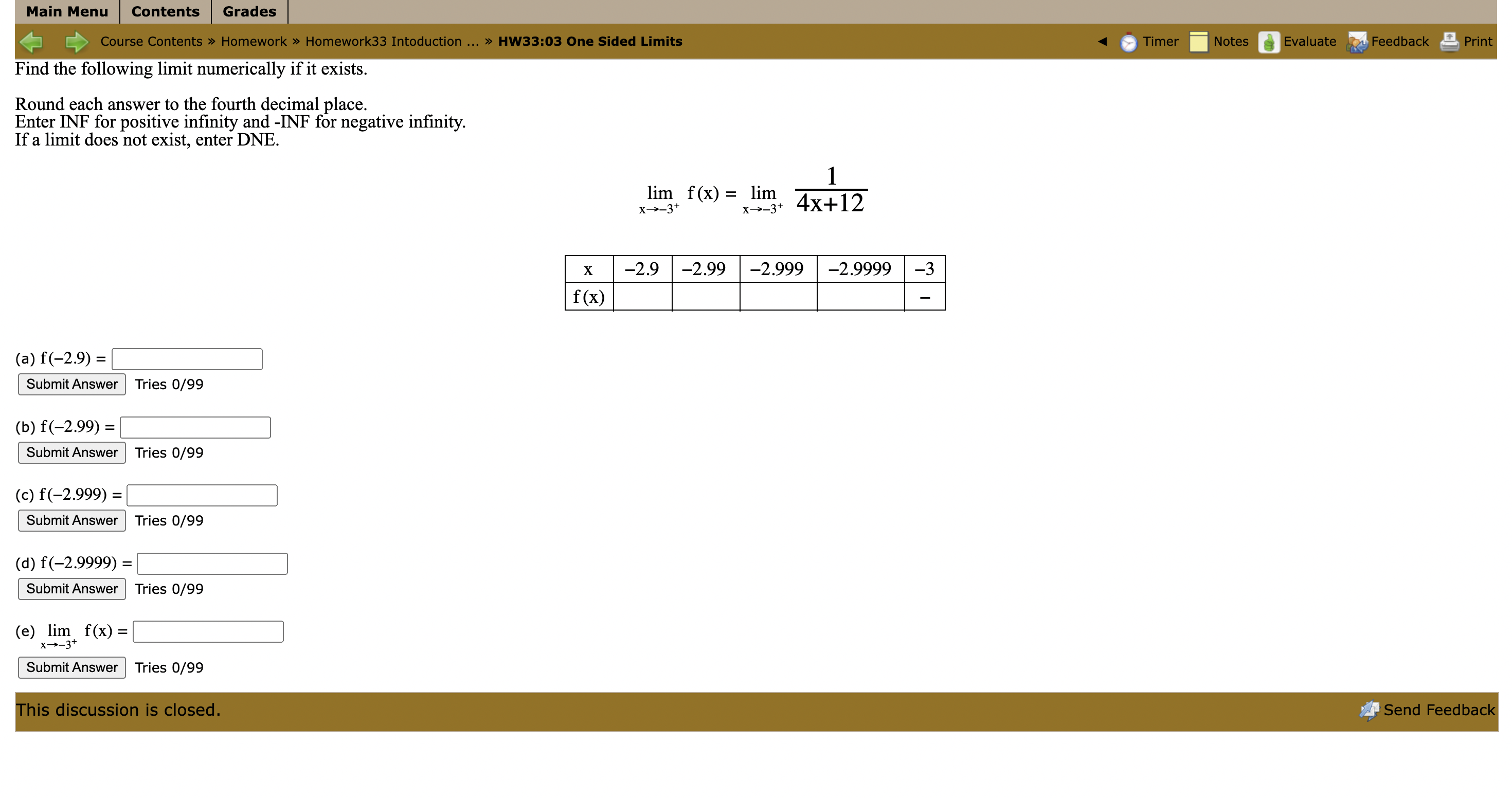
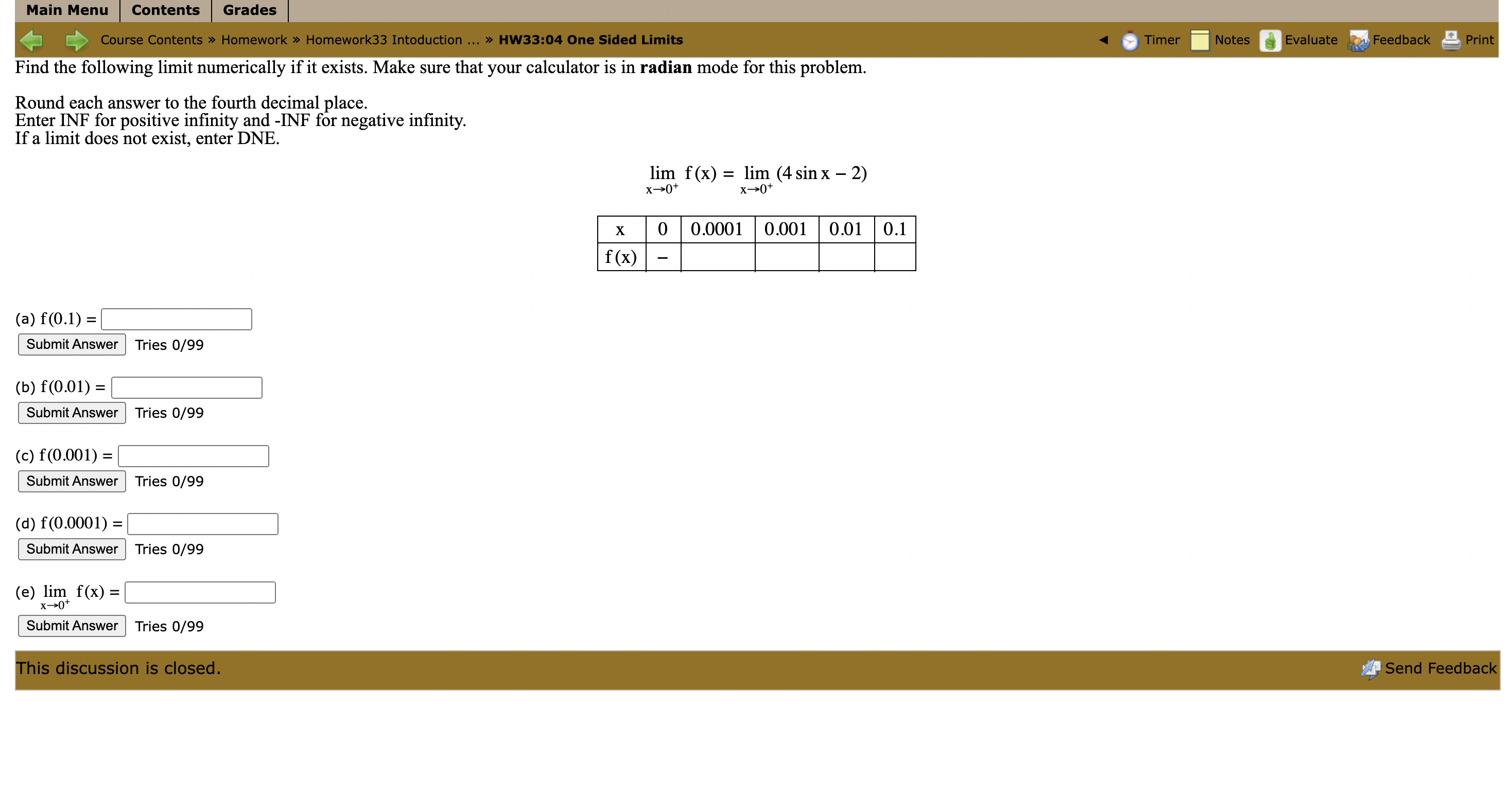
Find the following limit numerically if it exists. Make sure that your calculator is in radian mode for this problem. Round each answer to the fourth decimal place. Enter INF for positive infinity and -INF for negative infinity. If a limit does not exist, enter DNE.

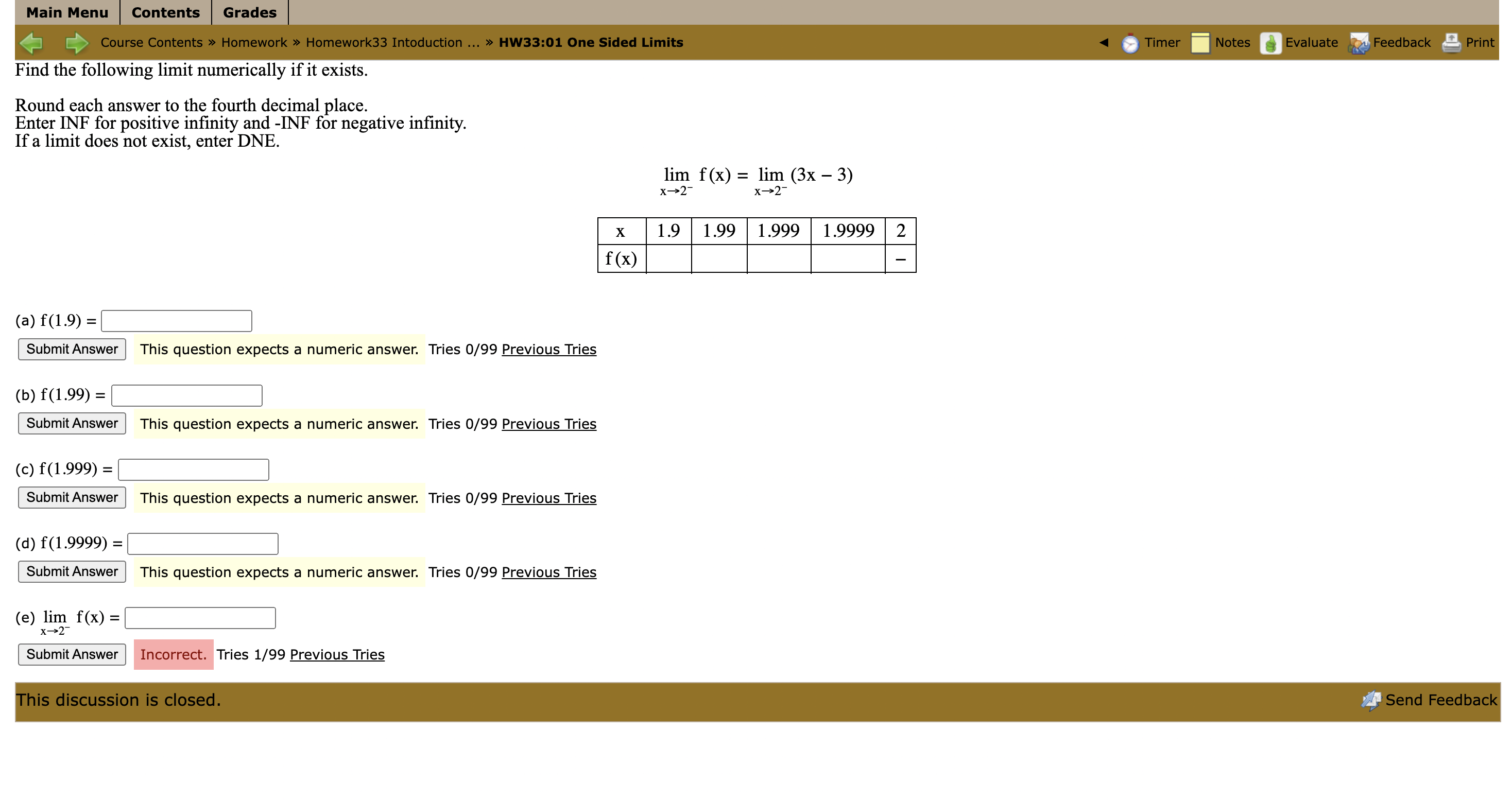
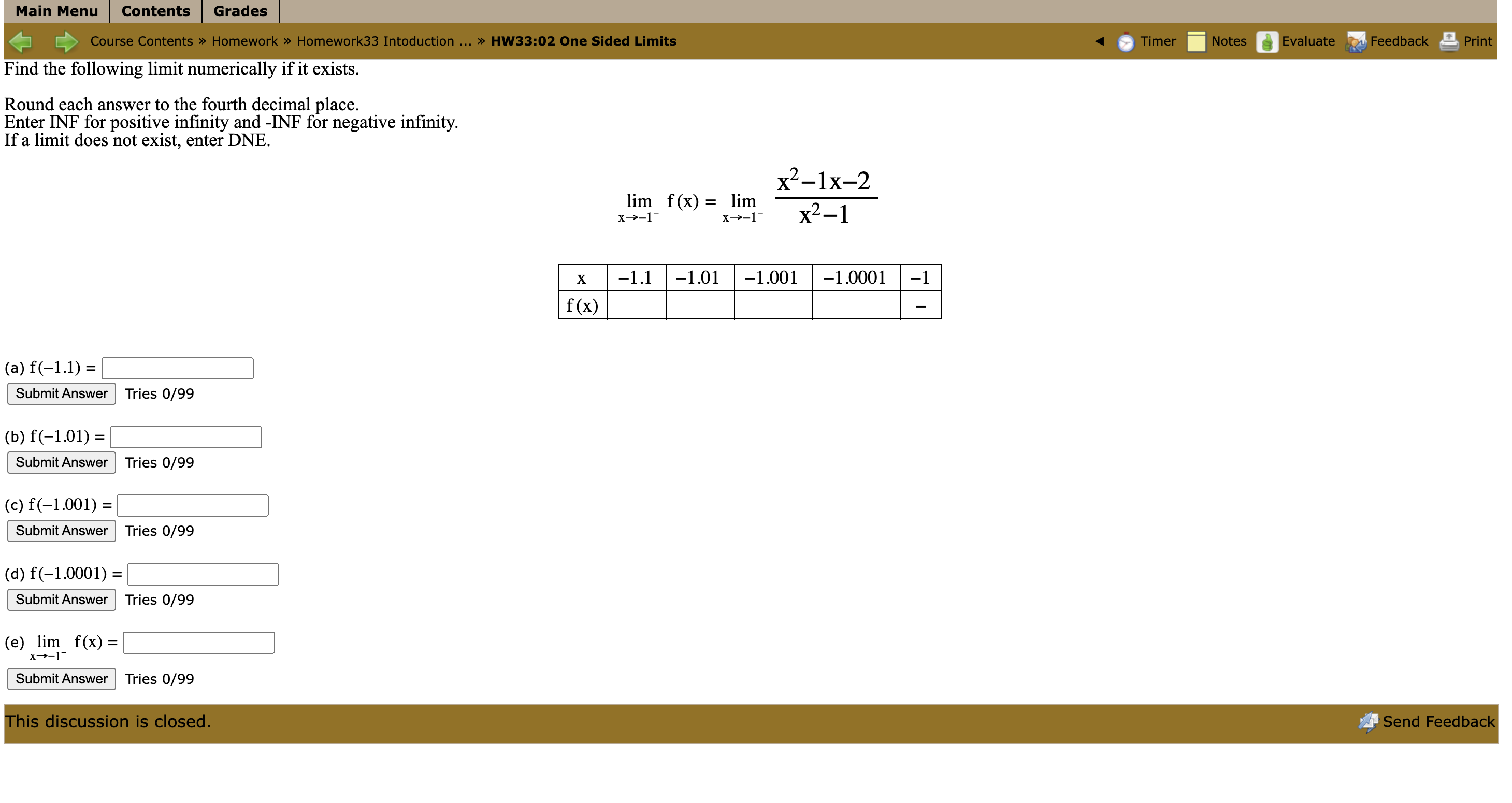
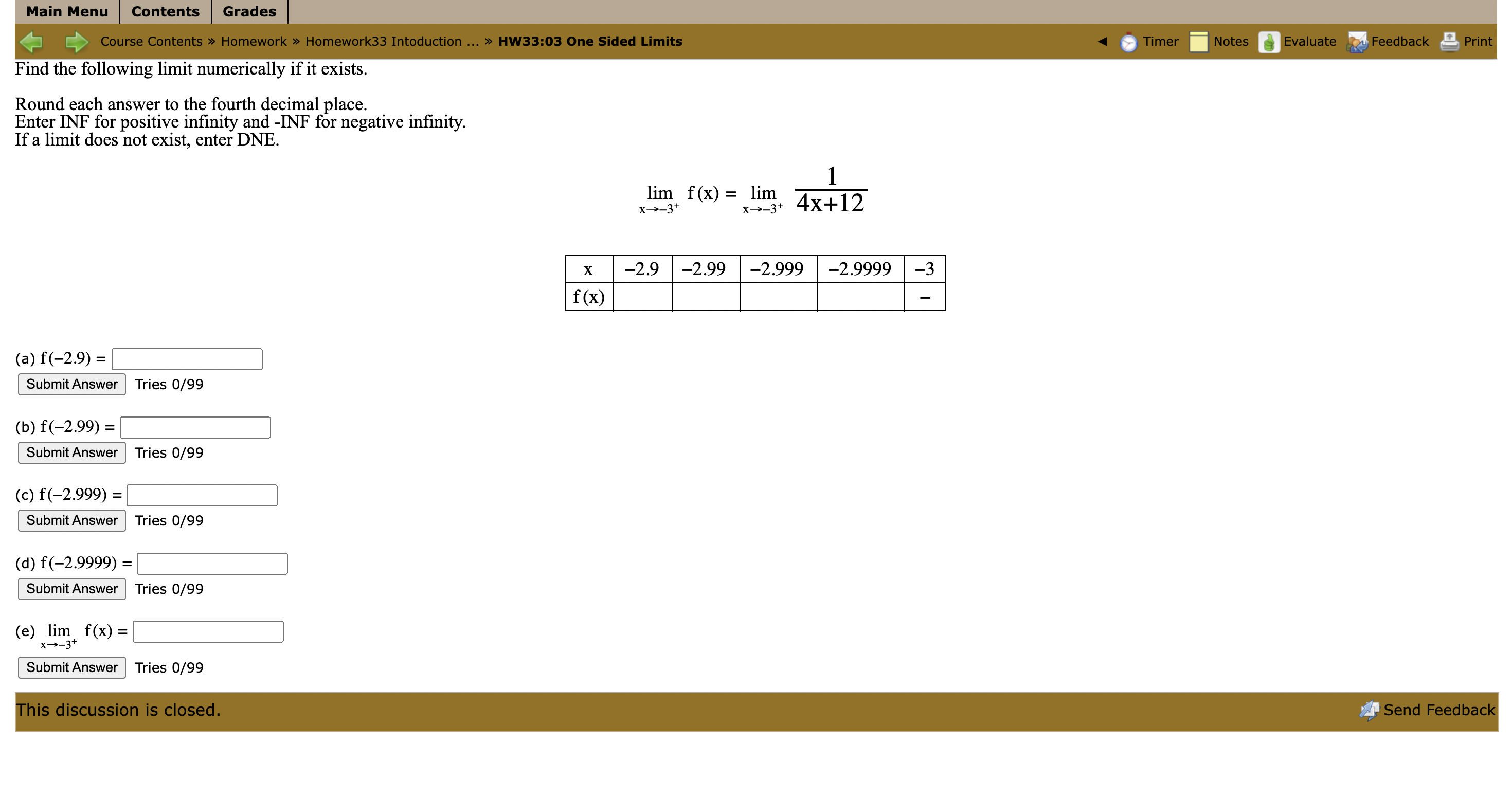
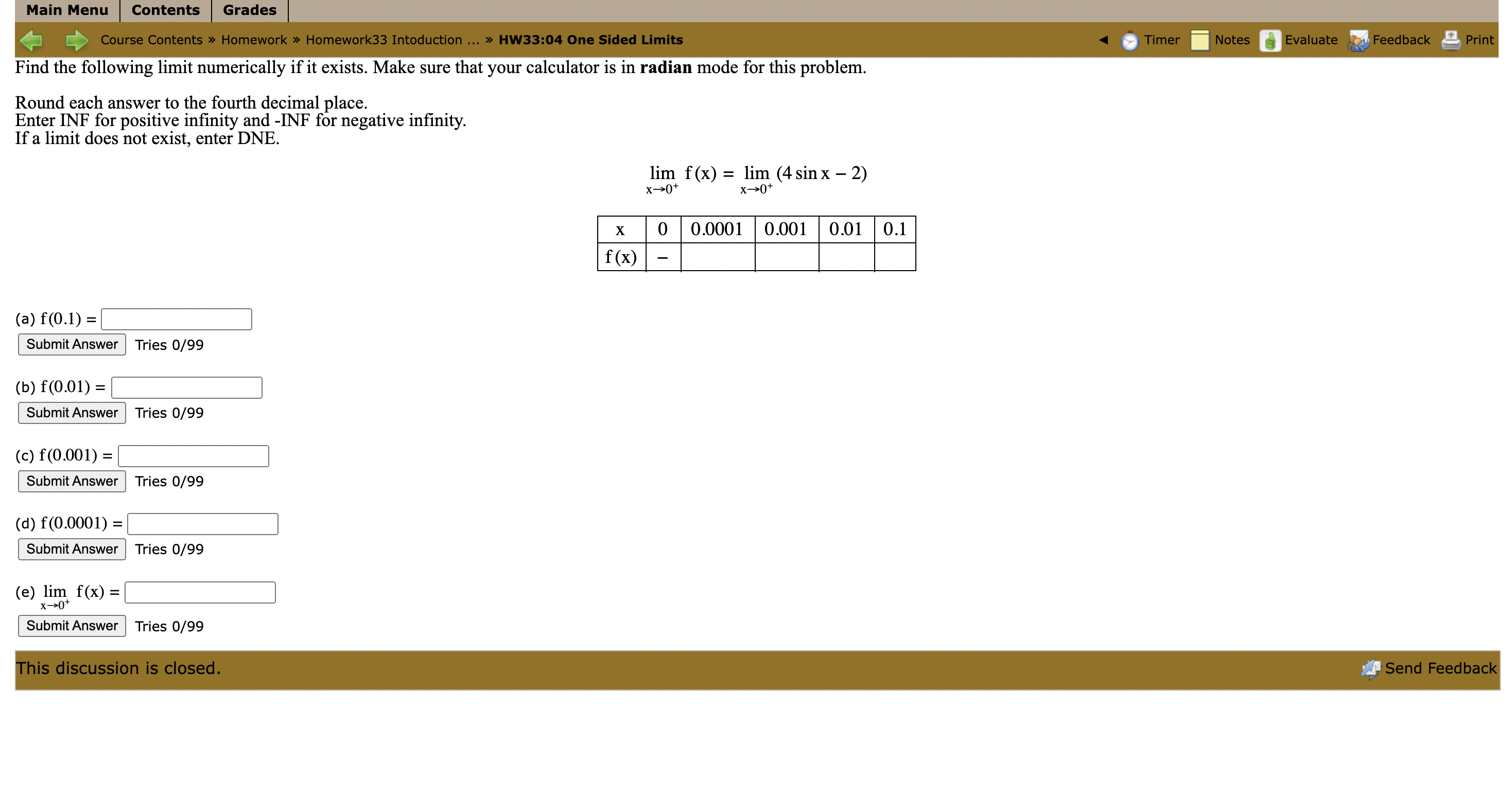
Main Menu Contents Grades [ Course Contents > Homework > Homework33 Intoduction ... > HW33:01 One Sided Limits Timer Notes Evaluate Feedback Print Find the following limit numerically if it exists. Round each answer to the fourth decimal place. Enter INF for positive infinity and -INF for negative infinity. If a limit does not exist, enter DNE. lim f (x) = lim (3x - 3) X -2- x->2 X 1.9 1.99 1.999 1.9999 2 f (x) (a) f(1.9) = Submit Answer This question expects a numeric answer. Tries 0/99 Previous Tries (b) f(1.99) = Submit Answer This question expects a numeric answer. Tries 0/99 Previous Tries (c) f(1.999) = Submit Answer This question expects a numeric answer. Tries 0/99 Previous Tries (d) f(1.9999) = Submit Answer This question expects a numeric answer. Tries 0/99 Previous Tries (e) lim f(x) = 1-2 Submit Answer Incorrect. Tries 1/99 Previous Tries This discussion is closed. Send FeedbackMain Menu | Contents Grades Course Contents > Homework > Homework33 Intoduction ... > HW33:02 One Sided Limits Timer Notes Evaluate Feedback Print Find the following limit numerically if it exists. Round each answer to the fourth decimal place. Enter INF for positive infinity and -INF for negative infinity. If a limit does not exist, enter DNE. x2-1x-2 lim f(x) = lim X->-1 - X->-1- x2-1 X -1.1 -1.01 -1.001 -1.0001 -1 f (x) (a) f(-1.1) = Submit Answer Tries 0/99 (b) f(-1.01) = Submit Answer Tries 0/99 (c) f(-1.001) = Submit Answer Tries 0/99 (d) f(-1.0001) = Submit Answer Tries 0/99 (e) lim f(x) = x->-1 Submit Answer Tries 0/99 This discussion is closed. Send FeedbackMain Menu Contents Grades [ Course Contents > Homework > Homework33 Intoduction ... > HW33:03 One Sided Limits Timer Notes Evaluate Feedback Print Find the following limit numerically if it exists. Round each answer to the fourth decimal place. Enter INF for positive infinity and -INF for negative infinity. If a limit does not exist, enter DNE. 1 lim f(x) = lim x - -3+ x - > -3+ 4x+12 X -2.9 -2.99 -2.999 -2.9999 -3 f(x) (a) f(-2.9) = Submit Answer Tries 0/99 (b) f(-2.99) = Submit Answer |Tries 0/99 (c) f(-2.999) = Submit Answer Tries 0/99 (d) f(-2.9999) = Submit Answer Tries 0/99 (e) lim f(x) = - 3+ Submit Answer Tries 0/99 This discussion is closed. Send FeedbackMain Menu Contents Grades Course Contents > Homework > Homework33 Intoduction ... > HW33:04 One Sided Limits Timer Notes Evaluate Feedback Print Find the following limit numerically if it exists. Make sure that your calculator is in radian mode for this problem. Round each answer to the fourth decimal place. Enter INF for positive infinity and -INF for negative infinity. If a limit does not exist, enter DNE. lim f (x) = lim (4 sin x - 2) x-+0+ x -+ 0+ X 0 0.0001 0.001 0.01 0.1 f (x) (a) f(0.1) = Submit Answer Tries 0/99 (b) f(0.01) = Submit Answer Tries 0/99 (c) f(0.001) = Submit Answer Tries 0/99 (d) f(0.0001) = Submit Answer Tries 0/99 (e) lim f(x) = x-0 Submit Answer Tries 0/99 This discussion is closed. Send Feedback