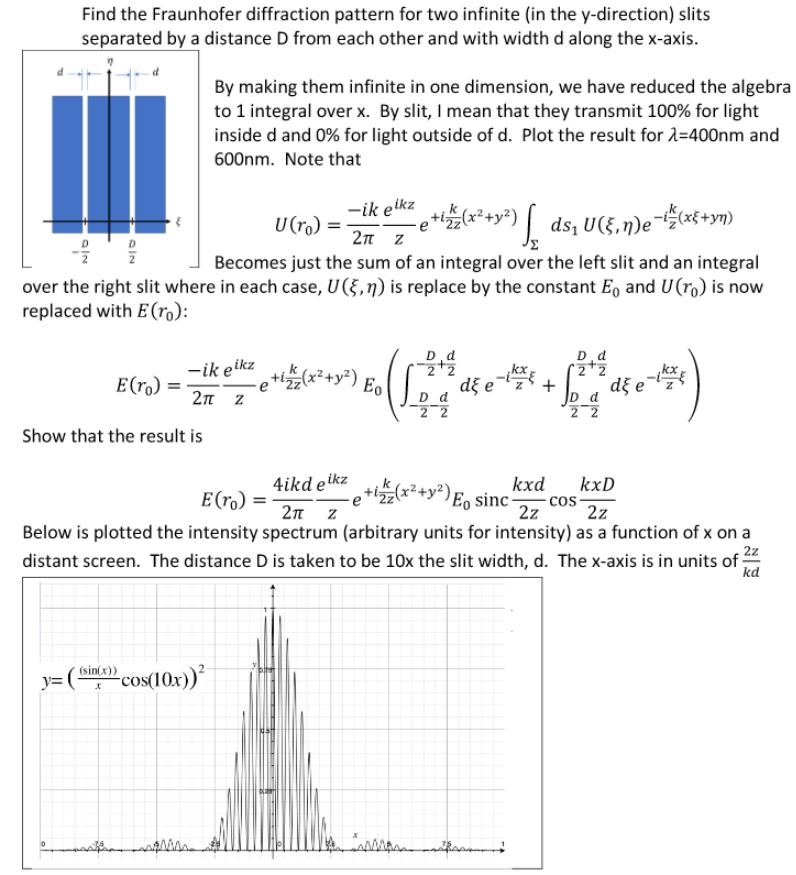
Find the Fraunhofer diffraction pattern for two infinite (in the y-direction) slits separated by a distance D from each other and with width d along the x-axis. By making them infinite in one dimension, we have reduced the algebra to 1 integral over x. By slit, I mean that they transmit 100% for light inside d and 0% for light outside of d. Plot the result for a=400nm and 600nm. Note that -ik eikz U(ro) = ds, U(,n)exf+yn) 2n z Becomes just the sum of an integral over the left slit and an integral over the right slit where in each case, U(},n) is replace by the constant E, and U(ro) is now replaced with E(ro): D,d -ik eikz (x+y) d e D d 2 2 E(r.) = Eo d e D d 2 2 2n z Show that the result is 4ikd eikz +ix+y) Eo sinc- kxd kxD E(ro) = cos- 2n z 2z 2z Below is plotted the intensity spectrum (arbitrary units for intensity) as a function of x on a 2z distant screen. The distance D is taken to be 10x the slit width, d. The x-axis is in units of kd (sin(x)) cos(10x)) y=