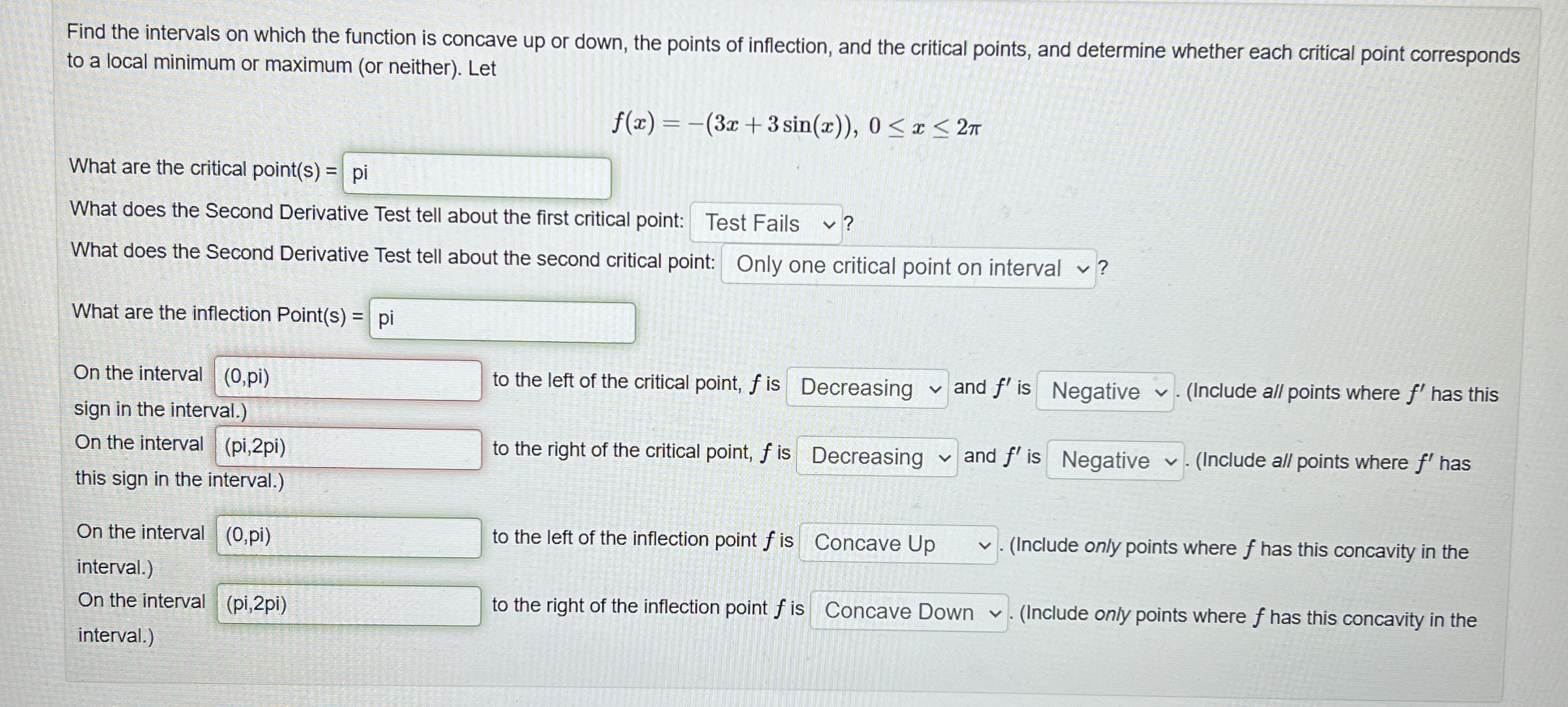
Question: Find the intervals on which the function is concave up or down, the points of inflection, and the critical points, and determine whether each critical
Find the intervals on which the function is concave up or down, the points of inflection, and the critical points, and determine whether each critical point corresponds to a local minimum or maximum or neither Let
What are the critical points
What does the Second Derivative Test tell about the first critical point:
What does the Second Derivative Test tell about the second critical point
What are the inflection Points
On the interval to the left of the critical point, is and is Include all points where has this sign in the interval.
On the interval this sign in the interval. to the right of the critical point, is Decreasing and is Include all points where has
On the interval to the left of the inflection point is Include only points where has this concavity in the interval. On the interval to the right of the inflection point is interval. Include only points where has this concavity in the
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


