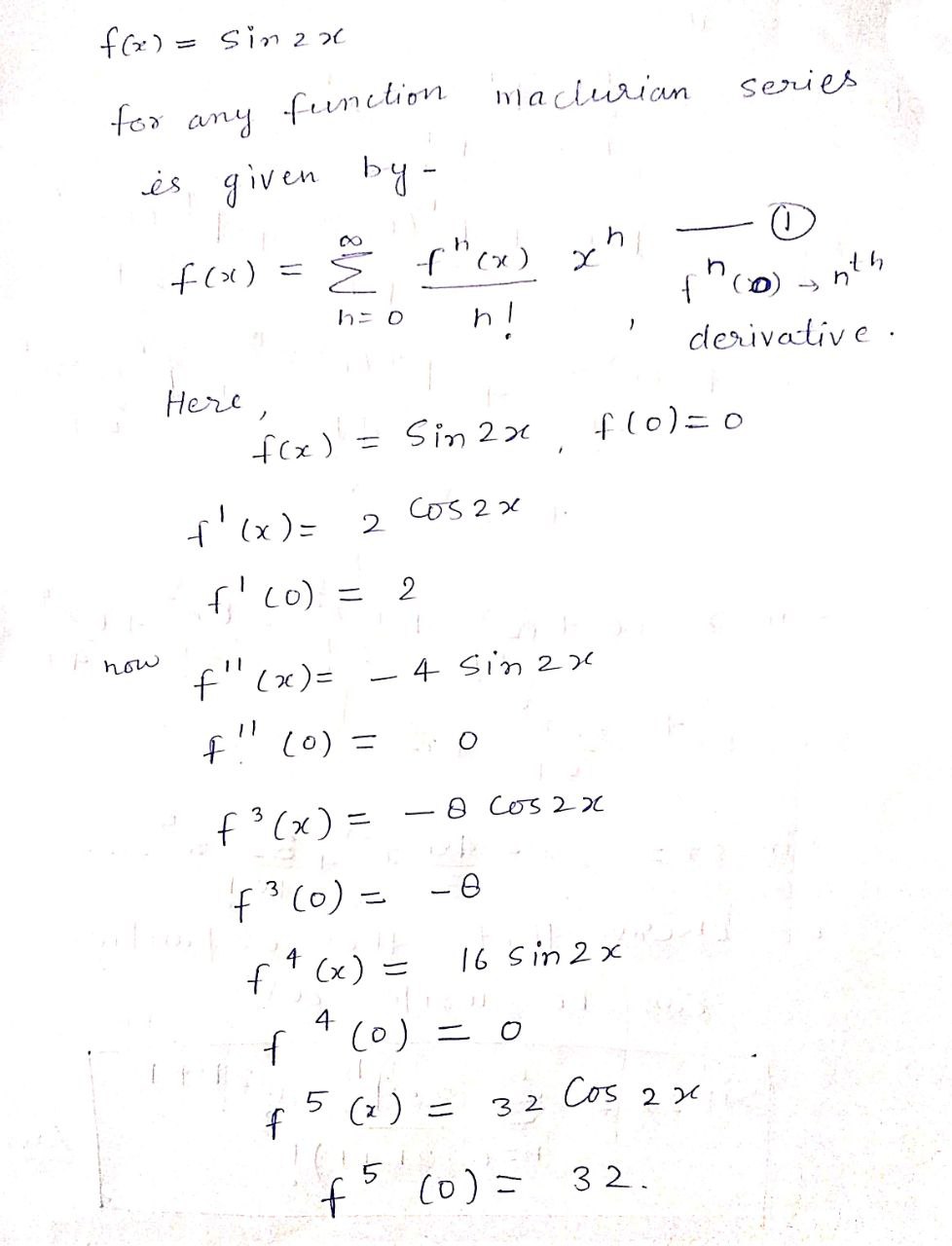
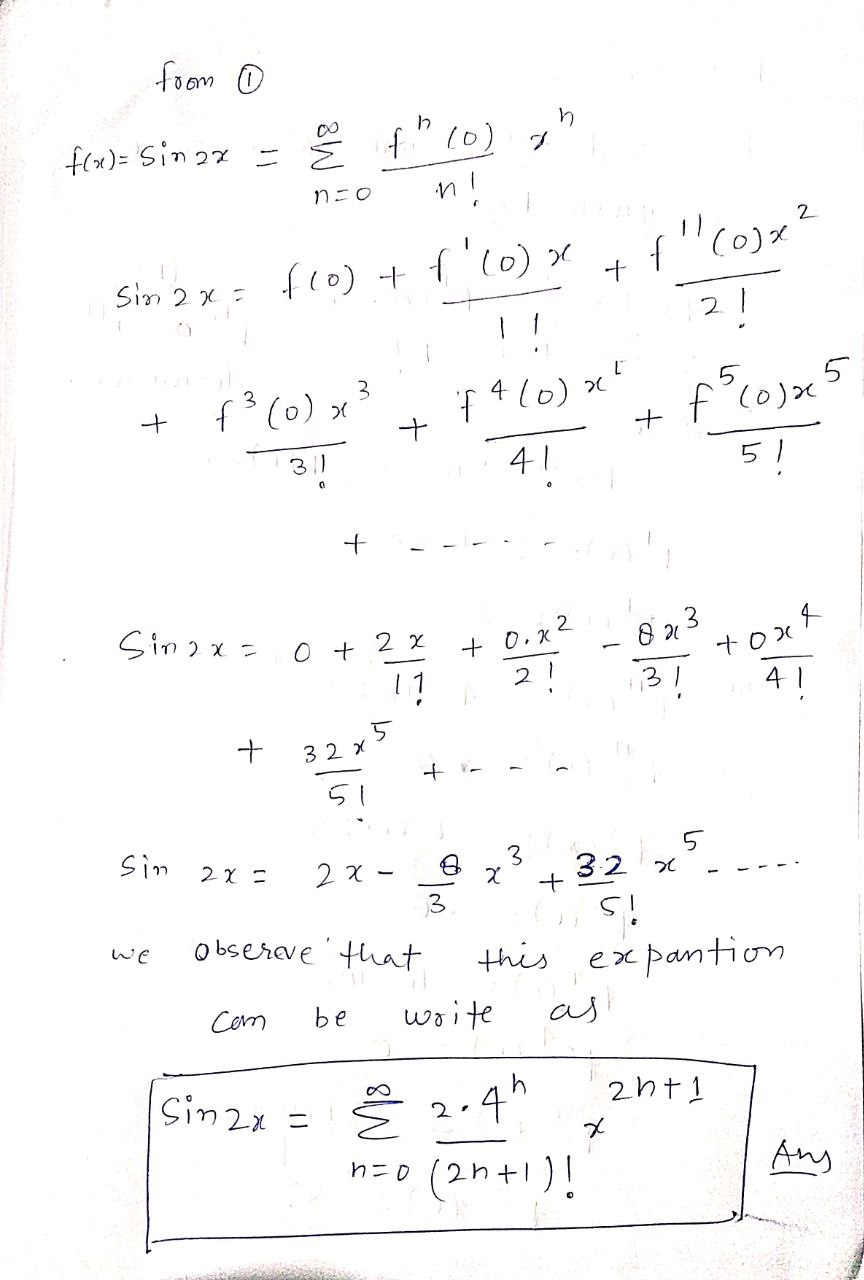
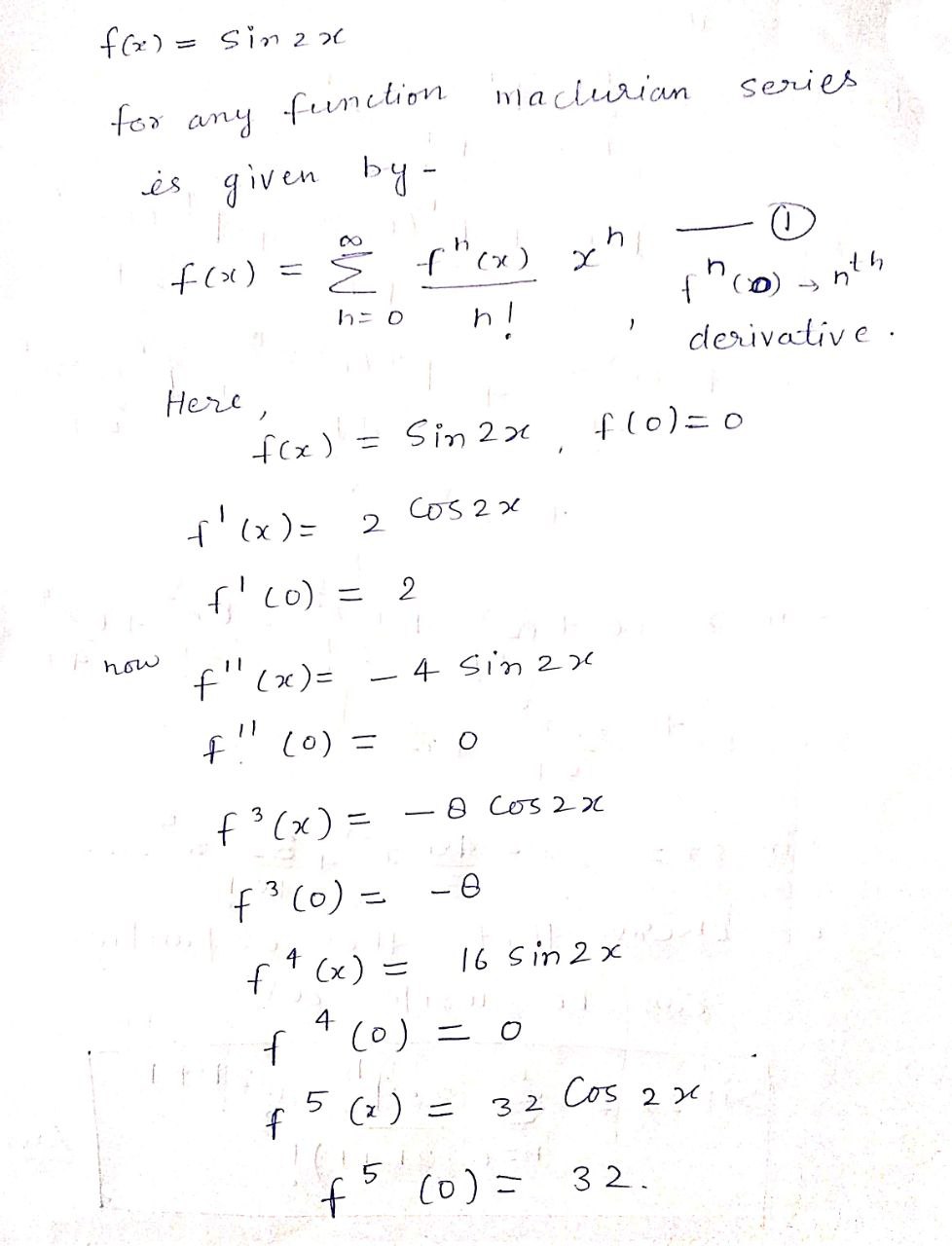
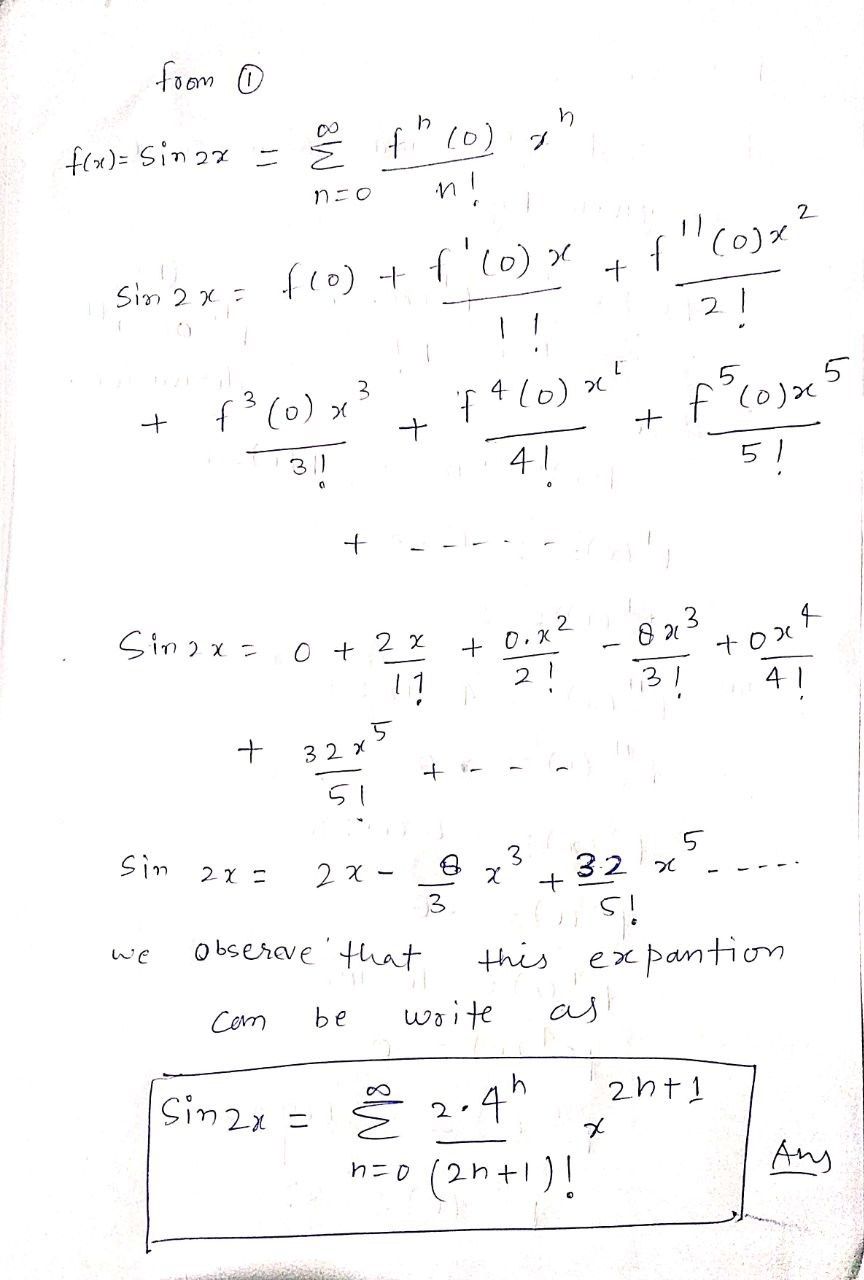
Find the Maclaurin series for the function. (Use the table of power series for elementary functions.) f(x) = sin(2x) F( x ) = n =f ( x ) = sin 2 20 for any function machurian series is given by - f ( x1 ) = 5 f" (x ) X h h = 0 (0) - nith n ! 1 derivative. Here f ( x ) = Sin 2 x f (0 ) = 0 1 ( x ) = 2 605 2 x f ' ( 0 ) = 2 I now f ( 20 ) = - 4 Sin 2 20 F ( 0 ) = 0 f 3 ( x ) = - 8 Cos 2 x f 3 (0 ) = - 0 f. ( x ) = 16 5in 2 x f * 4 (0 ) = 0 $ 5 ( x ) = 3 2 Cos 2 X f ( 0 ) = 32 .from 1 f ( x ) = Sin 2x = = f (0 ) ,7 n= 0 Sin 2x = ((0) + 1 (0) _ f cox 2 ! 1 1 1 + f 3 ( 0 ) x 3 f 4 ( 0 ) x 1 + + f cojoc 5 31 1 4 1 5 / + Sing x = 0+ 2x + 0 . x 2 8 2 3 1 1 2 1 131 4 1 + 32 x 5 5 Sin 2x = 2x - 3 5 X + 32 x - - . 3 we observe that this expantion Comn be write as Sin zx = 1 2. 4h 2h+1 X h= o ( 2h +1 ) ! Any