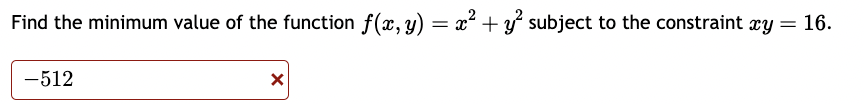
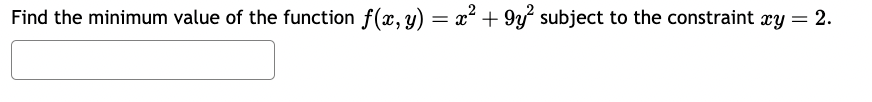
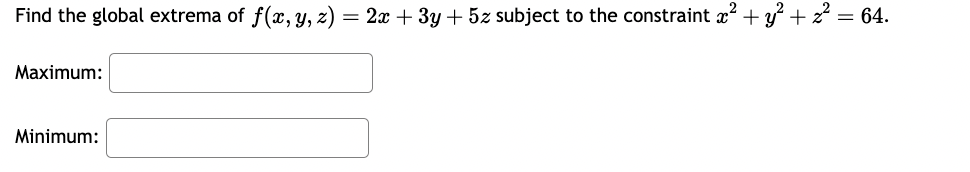
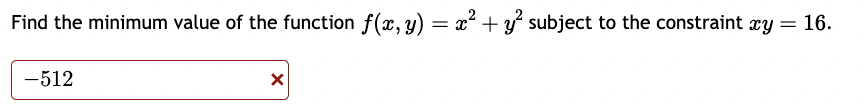
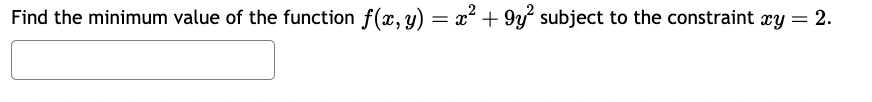
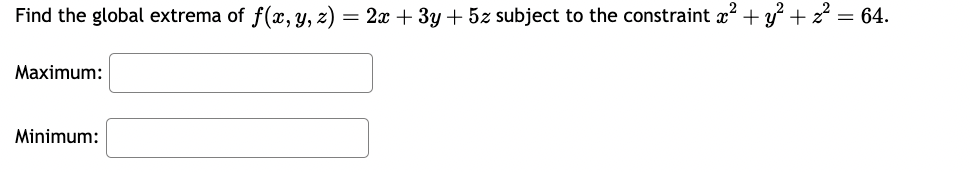
Find the minimum value of the function f(:l:, y) = 2:2 + y2 subject to the constraint my = 16. 512 X Find the minimum value of the function f(:::, y) = 23-2 + 93} subject to the constraint my = 2. Find the absolute extreme values of f(:L', y, z) = a: + 41!; + 82 subject to m2 + y2 + 2:2 = 16. 1. Absolute minimum of x, y, z) is ' ' 2. Absolute maximum of f(:1:,y, 2:) is ' ' A firm manufactures a commodity at two different factories, Factory X and Factory Y. The total cost (in dollars} of manufacturing depends on the quantities, a: and 3; produced at each factory, respectively, and is expressed by the joint cost function: C(m, y) = 1:1?2 + my + 4y2 + 400 A} If the company's objective is to produce 1,800 units per month while minimizing the total monthly cost of production, how many units should be produced at each factory? (Round your answer to whole units, i.e. no decimal places.) To minimize costs, the company should produce: at Factory X and at Factory Y B) For this combination of units, their minimal costs will be dollars. (Do not enter any commas in your answer.) A chemical manufacturing plant can produce 2: units of chemical 2 given 12 units of chemical P and 1' units of chemical R, where: Z : 180p0'75T0'25 Chemical P costs $100 a unit and chemical R costs $500 a unit. The company wants to produce as many units of chemical Z as possible with a total budget of $30,000. A) How many units each chemical (P and R) should be "purchased" to maximize production of chemical 2 subject to the budgetary constraint? Units of chemical P, 'p = Units of chemical R, T = B) What is the maximum number of units of chemical Z under the given budgetary conditions? (Round your answer to the nearest whole unit.) Max production, z: units Find the minimum cost of a rectangular box of volume 170 cm whose top and bottom cost 9 cents per cm and whose sides cost 7 cents per cm2. Cost = cents.Find the global extrema of at, y, z) = 2:: + 3y + 52: subject to the constraint 2:2 + 9'2 + 2:2 = 64. Maximum: ' ' Minimum: ' ' Find the maximum and minimum values of the function f(:r:,y) = mzy subject to 2x2 + 4y2 = 24 Please show your answers to at least 4 decimal places. Enter DNE if the value does not exist. Maximum value: ' ' Minimum value