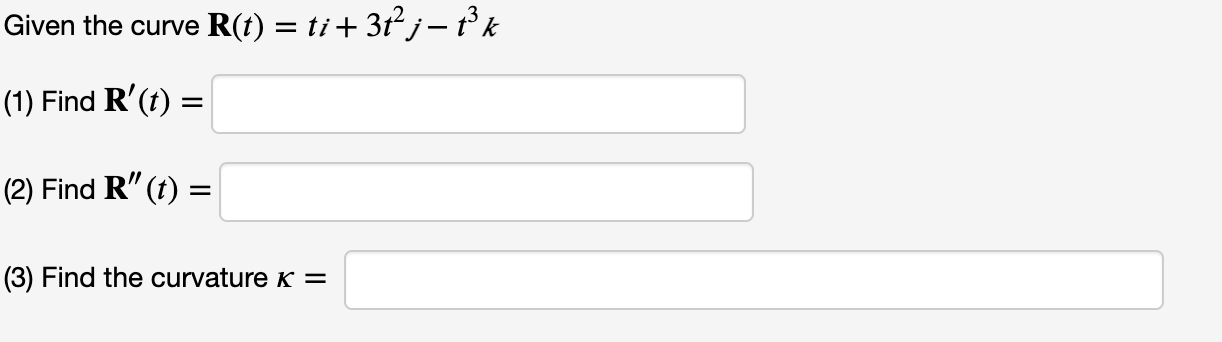
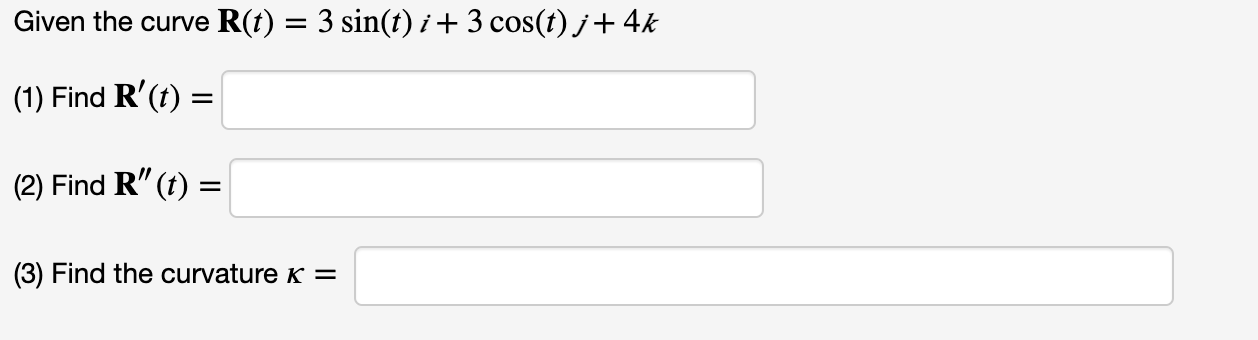
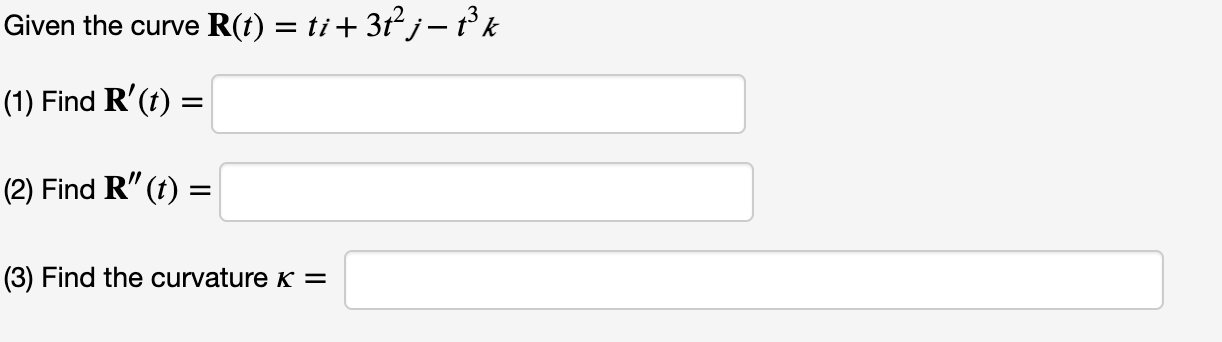
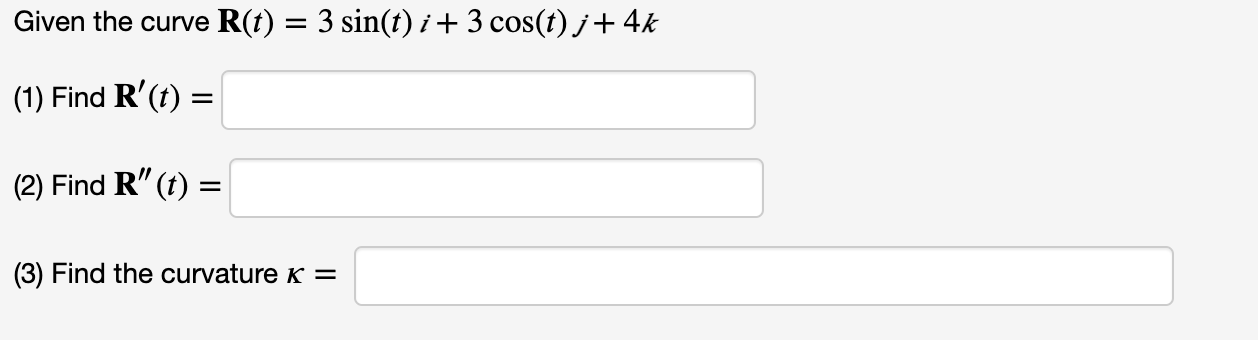
Find the position vector R(t) given the velocity V(t) = 492'1' + 20 c0s(5t)j+ lOIkand the initial position vector R(O) = 31' 2f 3/6. Find the position vector R(t) and velocity V(t) given the acceleration A(t) = 125e5'1' + 125 605(51') j+ 121% and the initial velocity vector V(0) = i 2j+ kand initial position vector R(0) = 3i + 3j+ 2k. W!) = R(t) = Find the curvature x of the plane curve y = 2e* at x = 4. K =Given the curve R(t) = ti + 312 j- 13 k (1) Find R'(t) = (2) Find R" (t) = (3) Find the curvature K =\fFind the position vector R(t) given the velocity V(t) = (4t + 3) / + 6 sin(3t) ; + 8t and the initial position vector R(0) = i - 3j + k. R(t) =