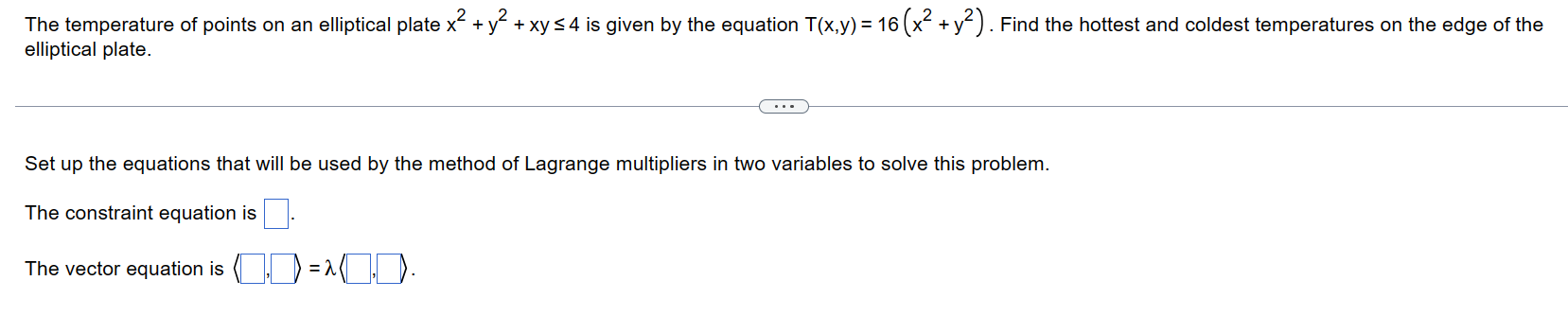
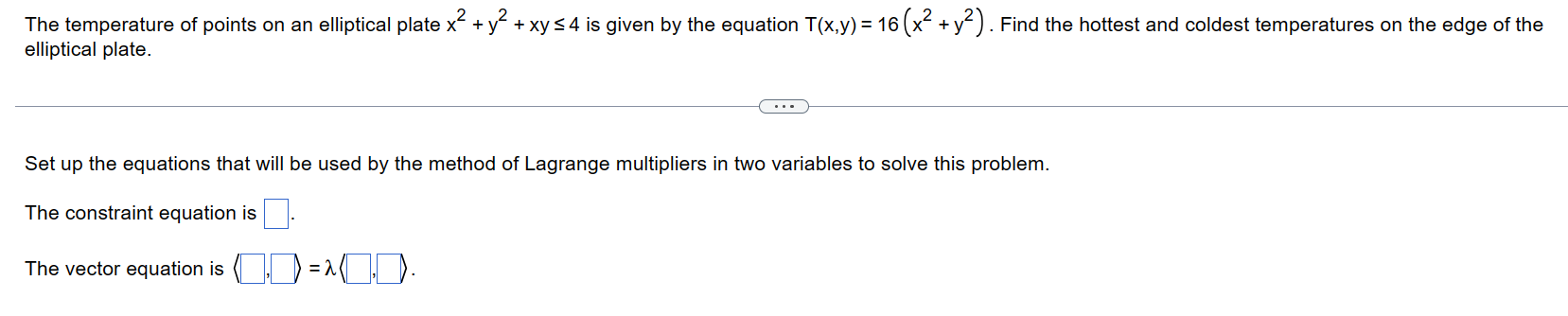
Find the values oft and g with [2 D and g 2 O that maximize the following utility function subject to the given constraint. Give the value of the utility function at the optimal point. u =f(l!,g) = .3!\"ng subject to 4r+ 29 = 54 What are the values of if and g at the optimal point? [: :9: Find the values of { and g with 12 0 and g 2 0 that maximize the following utility function subject to the given constraint. Give the value of the utility function at the optimal point. U = f(1,g) = 81 /2g1/2 subject to 31 + 6g = 18 . . . What are the values of { and g? 1 = ,9=Find the values of { and g with 12 0 and g 2 0 that maximize the following utility function subject to the given constraint. Give the value of the utility function at the optimal point. U = f(1,g) = $1/8g/8 subject to 51 + 7g = 35 . . . What are the values of { and g at the optimal point? 1 = , 9=[Find the absolute maximum and minimum values off(x,y) = X2 + 4V2 +4 over the region R = {(x,y) : x2 + 4y2 51}. Use Lagrange multipliers to check for extreme points on the boundary. Set up the equations that will be used by the method of Lagrange multipliers in two variables to nd extreme points on the boundary. The constraint equation, g(x,y) = 0 uses the function g(x,y) = D. D. The vector equation is , D = A The temperature of points on an elliptical plate X2 + y2 + xys 4 is given by the equation T(x,y) = 16 (x2 + yz) . Find the hottest and coldest temperatures on the edge of the elliptical plate. Set up the equations that will be used by the method of Lagrange multipliers in two variables to solve this problem. The constraint equation is V II >9 v The vector equation is (